noone___'s blog
0%

42801202-AGC017

发表于 更新于 分类于
AGC017

D

一个 $N$ 节点的树，两人轮流选择一条树上的边并断开，删除不包含 $1$ 号点的连通块，当一人不能操作时输，求胜者

树上 $\text{nim}$ 游戏，每个节点的 $\text{sg}$ 值是所有儿子 $\text{sg}$ 值 $+1$ 的异或和，判断根节点 $\text{sg}$ 函数值是否为 $1$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
const int N=1e5+100;
int n;
vector<int> G[N];

int dfs(int x,int fa=0){
    rei res=0;
    for(int y:G[x]) if(y!=fa) res^=dfs(y,x)+1;
    return res;
}

int main(){
    scanf("%d",&n);
    for(rei i=1,u,v;i<n;++i) scanf("%d%d",&u,&v),G[u].push_back(v),G[v].push_back(u);
    puts(dfs(1) ? "Alice" : "Bob");
    getchar(),getchar();
    return 0;
}

E

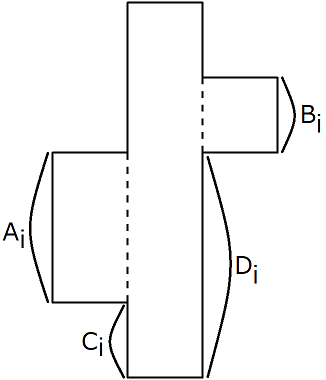
有 $n$ 块不规则拼图，每块拼图看成连接在一起的三个宽度为 $1$ 的矩形，如图https://atcoder.jp/img/agc017/2b6cd7f4500d3621bc18de407f167522.png
具体地，其中中间的矩形的高度为 $H$ ，左侧矩形的高度为 $A_i$ ，距离中间矩形底部 $C_i$ ，右侧矩形的高度为 $B_i$ ，距离中间矩形底部 $D_i$
将这些拼图放入一个边长为 $10^{100}$
的正方形中，需要满足如下条件：

  • 所有 $N$ 块拼图都必须用上

  • 所有拼图的中间矩形的下底面需要和正方形的下底面对齐

  • 对于非中间的部分的下底面，要么和正方形的下底面对齐，要么和另一块拼图的非中间部分的上顶面对齐

  • 拼图只能平移，不能旋转或翻转

对于一块拼图，如果其一侧的小矩形不接地，那么这个小矩形一定与另一拼图接地的小矩形相接，即，其高度无关紧要，只关心非 “接地” 小矩形的 $C_i,D_i$

而对于接地的小矩形有 $C_i=0 / D_i=0$ ，此时需要关注高度

于是，对于每块拼图的一侧，我们可以给它对应到个参数：如果是接地的，称它是 $下A_i$ 或 $下B_i$ ，否则，称它为 $上C_i$或 $上D_i$

显然有： $上x$ 的一侧与某矩形 $下x$ 相接，且最两端矩形的两侧是 $下x$

考虑到 $上下x$ 相连没有什么好性质，不妨利用左右矩形：对于左侧小矩形，点 $N_x$ 表示 $上x$ ，点 $P_x$ 表示 $下x$ ；右侧矩形则相反，点 $P_x$ 表示 $上x$ ，点 $N_x$ 表示 $下x$

两个拼图的连接处就是相同的点：全为 $P_x$ 或全为 $N_x$

那么，对于拼图 $(u,v)$ 连接 $u\rightarrow v$ ，那么一连串拼图构成的组对应所得的图上的一条有向边，且路径起点为 $P_x$ ，终点为 $N_x$

那么转化为判断整张图是否能被拆分成若干个从 $P_x$ 连向 $N_x$ 的有向路径即可

考虑建立超级点 $S$ ，能向所有形如 $P_x$ 的点不断提供入边，也能使足够多的 $N_x$ 连向它

那么对于路径 $P_x\rightarrow v_1\rightarrow v_2\rightarrow …\rightarrow N_y$ ，在两侧分别补上 $N_y\rightarrow S$ 和 $S\rightarrow P_x$ ，如此得到一个有向圈

那么在连接若干条与 $S$ 的边后，图 $G$ 将变为 $\text{Euler}$ 图

考虑到 $\text{Euler}$ 图的性质: $\forall v\in G , 有 d^+(v)=d^-(v)$

由此：在删去 $S$ 及其关联的边后， $\forall P_x\in G , 有d^-(P_x)\leq d^+(P_x)$ ，$\forall N_x\in G , 有d^-(N_x)\geq d^+(N_x)$

首先，如果一张图满足上述条件，那么我们将 $S$ 点与若干个点连边后，可以得到一张 $\text{Euler}$ 图 (且这个方案事实上是唯一的，即我们可以算出 $S$ 该向每个点连多少条边)。

其次，由 $\text{Euler}$ 图的性质，可得到 $S$ 的若干条 $\text{Euler}$ 回路 (这里用若干的原因是 $G$ 不一定连通)。

那么，考虑其中的每个圈 (注意与回路的区别)：

  • 如果它经过 $S$ ，那么将 $S$ 点去掉后，就得到一个可行的路径。

  • 如果这个圈不经过点 $S$

    那么，如果这个圈可以和一个包含 $S$ 点的圈合并，得到一个大的回路，那么这个回路也满足条件，即，边不重复。于是，希望这些圈尽可能地进行合并

    所以，考虑最终得到的每个图的连通分量 ($\text{Euler}$ 图的强连通性保证这里的强连通分量和弱连通分量是同一个)，如果存在一个不包含 $S$ 的连通分量，则问题是无解的 —— 因为这个圈/回路不包含 $S$ ，从而不可能找到一条对应的路径经过 $S$ 和圈/回路中所有的边。

    而反之，如果所有连通分量都包含 $S$ (从而只有一个连通分量)，那么问题就是有解的了。

于是，我们使用并查集维护一下连通性就可以了。注意到，在满足性质的条件下，一个点和 $S$ 相连当且仅当它的入度和出度不相等。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
const int N=410;
int n,H,V;
int fa[N],in[N],out[N];
bool dicyc[N];

int get_anc(int x){return fa[x]==x ? x : fa[x]=get_anc(fa[x]);}

int main() {
    int Lu,Ld,Ru,Rd,L,R;
    scanf("%d%d",&n,&H); V=H<<1;
    iota(fa,fa+V,0);
    for(rei i=1;i<=n;++i){
        scanf("%d%d%d%d",&Lu,&Ru,&Ld,&Rd);
        ++out[ L=(Ld ? Ld+H : Lu)-1 ];
        ++in[ R=(Rd ? Rd : Ru+H)-1 ];
        fa[ get_anc(L) ]=get_anc(R);
    }
    rei i;
    for(i=0;i<H && in[i]<=out[i] && in[i+H]>=out[i+H];++i);
    if(i!=H) return puts("NO"),0;
    for(rei i=0;i<V;++i) dicyc[ get_anc(i) ] |= in[i]!=out[i] || !in[i];
    for(i=0;i<V && (fa[i]!=i || dicyc[i]);++i);
    puts(i==V ? "YES" : "NO");
    getchar(),getchar();
    return 0;
}

F

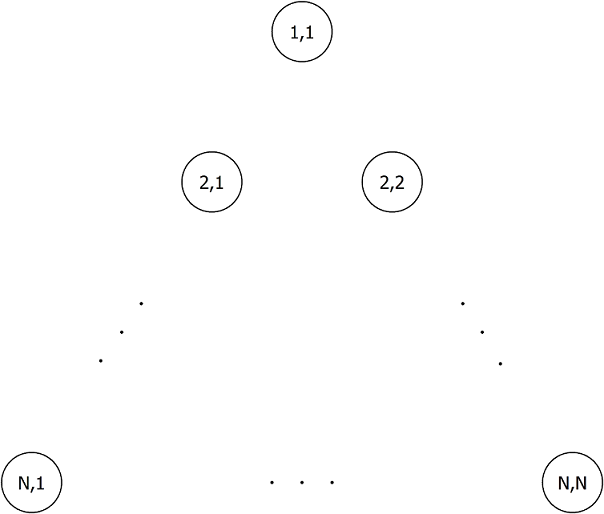
你有一个由 $\frac{n(n+1)}{2}$ 个点组成的等边三角形。 在 $(i,j)$ 点左下的是 $(i+1,j)$ 点， 右下的是 $(i+1,j+1)$ 点. 现在在上面画 $m$ 条从 $(1,1)$ 开始，$(n,p)$ 结束的连续路径 $(p\in[1,n])$ ， 满足对于任意 $1\leq i\leq j\leq m$, 第 $j$ 条线的任意一个部分不在第 $i$ 条线的左边。
https://atcoder.jp/img/agc017/8d354fb1a389a0aa5b64ba93f6ca7801.png
另外，还有 $k$ 个限制 , 第 $i$ 个限制形如 $A_i,B_i,C_i$ ，表示第 $A_i$ 条路径， 在第 $B_i$ 次决策的时候， 如果 $C_i=0$ ​则必须走左下， 否则必须走右下。

求出一共有多少种不同的画路径的方案满足以上的要求。

有一个朴素状压 $\text{dp}$ ，用 $O(m\times 4^n)$ 直接枚举状态转移

而直接枚举状态显然多余考虑了很多不合法状态

有神仙思路如下：

设 $0$ 为向左走，$1$ 为向右走，不考虑方向的限制，合法转移后的状态一定满足任何一个前缀 $1$ 的个数都大于之前状态前缀 $1$ 的个数

那么设 $dp_{i,j,k}$ 表示第 $i$ 条路径的第 $j$ 条转移，转移状态的前 $j$ 位与 $k$ 相同，考虑向右的情况：直接把后面的第一个 $1$ 变为 $0$ ，然后提到前面，如此，中间段取 $1/0$ 都满足要求，不会向左越过原来的，总复杂度 $O(n\times m\times 2^n)$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
const int N=21;
const int mod=1e9+7;
int n,m,k,all,last=1,cur,ans;
int dir[N][N],dp[2][1<<N];

inline void fix(int &x){ x>=mod ? x-=mod : 0;}
inline int lowbit(int x){ return x&(-x);}

int main(){
    scanf("%d%d%d",&n,&m,&k);--n;
    all=(1<<n)-1;
    for(rei i=1,x,y,foo;i<=k;++i) scanf("%d%d%d",&x,&y,&foo),dir[x][y-1]=foo+1;
    dp[0][0]=1;
    for(rei i=1;i<=m;++i) for(rei j=0;j<n;++j){
        swap(last,cur);
        rei foo=1<<j,bar=all^((foo<<1)-1);
        for(rei s=0;s<=all;++s) dp[cur][s]=0;
        for(rei s=0;s<=all;++s){
            if(dp[last][s]){
                if(dir[i][j]!=2 && (!(foo&s))) fix(dp[cur][s]+=dp[last][s]);//左
                if(dir[i][j]!=1){//右
                    rei x;
                    if(foo&s) x=s;//必须右
                    else{
                        if(!(bar&s)) x=s|foo;
                        else x=(s|foo)^lowbit(bar&s);
                    }
                    fix(dp[cur][x]+=dp[last][s]);
                }
            }
        }
    }
    for(rei i=0;i<=all;++i) fix(ans+=dp[cur][i]);
    printf("%d\n",ans);
    getchar(),getchar();
    return 0;
}