noone___'s blog
0%

81801202-AGC013

发表于 分类于
AGC013

C

长度为 $l$ 的圆环上有 $n$ 个蚂蚁，位置为 $x_i$ ，运动方向为 $d_i$ ，$1$ 为顺时针，$2$ 为逆时针。每只蚂蚁同时开始以单位速度移动，若两蚂蚁相遇则会改变自身方向，求 $t$ 秒后每只蚂蚁位置

易知蚂蚁的相对位置不变，将相遇掉头看成交换编号，可以算出 $t$ 秒后的有蚂蚁的位置

记录第一只蚂蚁的 $rank$ ，对于每一只蚂蚁来说，每当一只蚂蚁倒着穿过， $rank—$ ；正着穿过 $rank++$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const int N=1e5+100;
int n,l,t,rank_1,rnk[N];
struct data{
    int x,w;
}a[N];

int main(){
    scanf("%d%d%d",&n,&l,&t);
    for(rei i=1;i<=n;++i){ scanf("%d%d",&a[i].x,&a[i].w); a[i].w==2 ? a[i].w=-1 : 0;}
    for(rei i=1;i<=n;++i){
        rei length=a[i].x+a[i].w*t;
        rank_1+=length/l;
        if(length%l<0) --rank_1;
        rnk[i]=(length%l+l)%l;
    }
    sort(rnk+1,rnk+1+n);
    rank_1=(rank_1%n+n)%n;
    // for(rei i=1;i<=n;++i) printf("%d ",rnk[i]);
    // printf("rank_1:%d\n",rank_1);
    for(rei i=rank_1+1;i<=n;++i) printf("%d\n",rnk[i]);
    for(rei i=1;i<=rank_1;++i) printf("%d\n",rnk[i]);
    getchar(),getchar();
    return 0;
}

D

盒子里有黑白两种颜色 $n$ 个球，进行 $m$ 次操作，每次操作：从盒子中任取一个球，向盒子里添加黑白球各一个，在任取一个球。初始的球颜色不给出，求取出的 $2m$ 个球有多少种颜色序列

本质上仅有四种操作：BB；BW；WB；WW

以操作次数为 $x$ 轴，盒子里白球数为 $y$ ，则有

https://cdn.luogu.com.cn/upload/image_hosting/ox2813ev.png

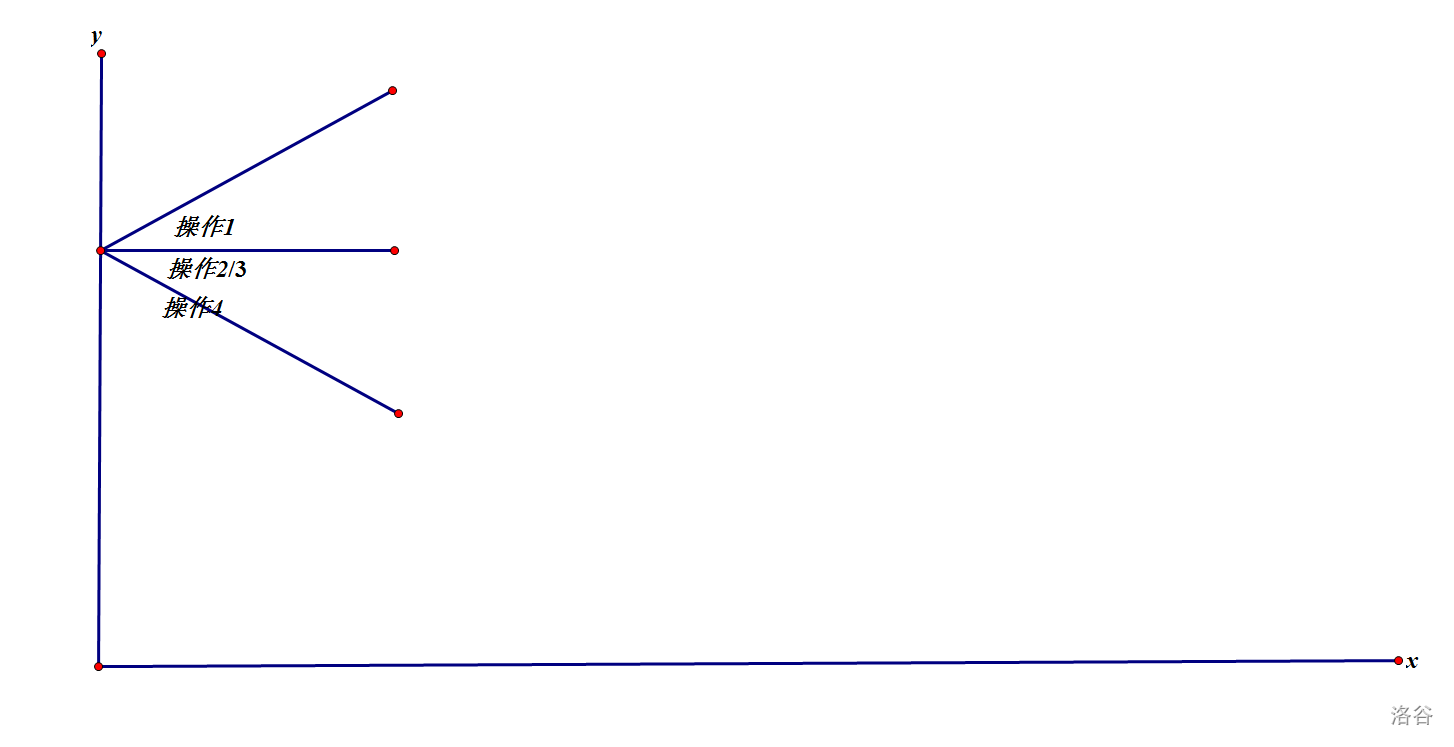
https://cdn.luogu.com.cn/upload/image_hosting/au35glpi.png

显然四种操作会形成 $4$ 种不同序列，以任一点为起点画个图

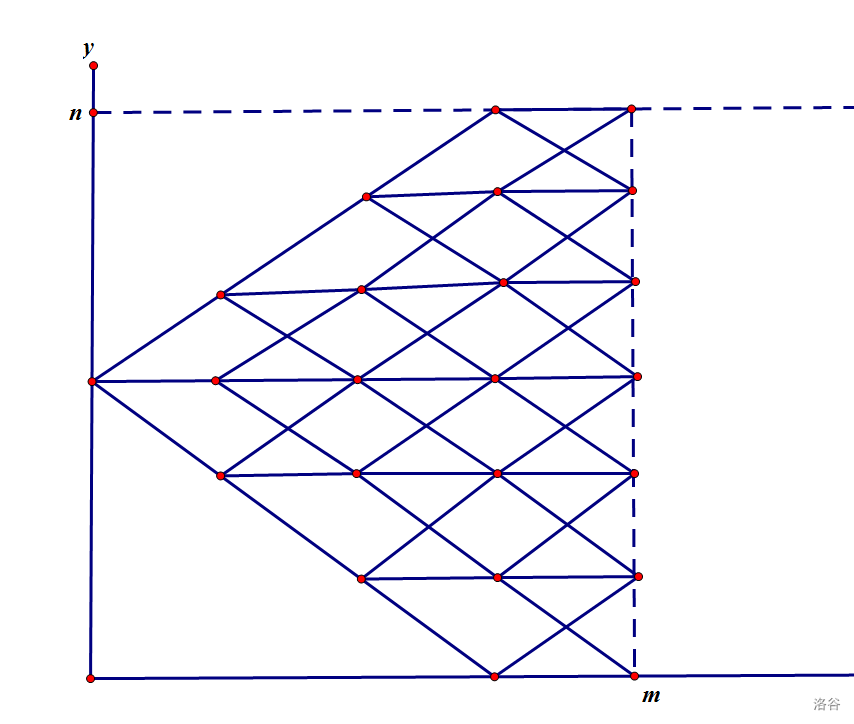
https://cdn.luogu.com.cn/upload/image_hosting/rprt0vu0.png

设状态 $f_{i,j}$ 表示操作 $i$ 次，盒子里有 $j$ 个白球时序列的情况

但注意以所有盒子里情况为起点时会存在操作相同且最终序列也相同的情况，有结论：只统计白球数量到达过 $0$ 的操作组即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
const int N=3010;
const int mod=1e9+7;
int n,m,f[N][N][2],ans;

inline void fix(int &x){ x>=mod ? x-=mod : 0;}

int main(){
    scanf("%d%d",&n,&m);
    for(rei i=1;i<=n;++i) f[0][i][0]=1; f[0][0][1]=1;
    for(rei i=0;i<m;++i)
        for(rei j=0;j<=n;++j){
            f[i][j][0]%=mod,f[i][j][1]%=mod;
            if(j-1>=0){
                if(j==1) fix(f[i+1][j-1][1]+=f[i][j][0]);
                else fix(f[i+1][j-1][0]+=f[i][j][0]);
                fix(f[i+1][j-1][1]+=f[i][j][1]);
                if(j==1) fix(f[i+1][j][1]+=f[i][j][0]);
                else fix(f[i+1][j][0]+=f[i][j][0]);
                fix(f[i+1][j][1]+=f[i][j][1]);
            }
            if(j+1<=n){
                fix(f[i+1][j+1][0]+=f[i][j][0]);
                fix(f[i+1][j+1][1]+=f[i][j][1]);
                fix(f[i+1][j][0]+=f[i][j][0]);
                fix(f[i+1][j][1]+=f[i][j][1]);
            }
        }
    for(rei i=0;i<=n;++i) fix(ans+=f[m][i][1]);
    printf("%d\n",ans);
    getchar(),getchar();
    return 0;
}

E

长度为 $n$ 的木板上有 $m$ 个标记点，距离木板左端点的距离分别为 $x_i$ ，在木板上放置一些不相交正方形满足：边长整数，底面紧贴木板，不能超出木板且覆盖所有木板，标记点的位置不能再两正方形交界处，记贡献为所有正方形面积的乘积，求出所有合法方案的贡献和

具体图例见原题

转化成神仙组合意义：

  • 在 $N+1$ 个间隔（包含位置为 $0$ 和 $N$ 的间隔）中放置若干个隔板。
  • 其中位置 $0$ 和 $N$ 必须放置隔板，且有 $M$ 个位置禁止放置隔板。
  • 对于 $N$ 个格子，每个格子中可以放球，蓝球或者红球。
  • 特别满足：在相邻两个隔板间的每个格子中，蓝球数恰为 $1$，红球数恰为 $1$

隔板对应正方形边界，对于长度为 $l$ 的段，放一个蓝球一个红球的方案数恰为 $l^2$

对于一种放置隔板的方案，放球的方案数为 $\prod_{i=1}^k (a_i)^2$ ，那么转化为统计放置隔板和球的方案数

设 $f_{i,j}$ 表示考虑前 $i$ 个格子和前 $i+1$ 个间隔，且最后一个隔板右边的球为 $j$ 个时发放置方案数

显然可以写出 $f[i+1]\leftarrow f[i]$ 的转移式子，取决于第 $i+1$ 个格子右侧是否进制放置隔板

  • 对于非标记点：

  • 对于标记点：

考虑到上述转移均为常系数齐次线性递推形式，故写成矩阵：

  • 对于非标记点

  • 对于标记点

即有 $N$ 个 $A$ 矩阵连乘，其中 $M$ 个被替换为 $B$ 矩阵，求一向量乘矩阵的结果

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
const int mod=1e9+7;
int n,m;

struct Matrix{
    ll a[3][3];
    Matrix(){ memset(a,0,sizeof a);}
    friend Matrix operator *(const Matrix &x,const Matrix &y){
        Matrix res;
        for(rei i=0;i<3;++i) for(rei j=0;j<3;++j) for(rei k=0;k<3;++k)
            res.a[i][j]+=x.a[i][k]*y.a[k][j];
        for(rei i=0;i<3;++i) for(rei j=0;j<3;++j) res.a[i][j]%=mod;
        return res;
    }
};

int main(){
    Matrix A,B,ans;
    ans.a[0][0]=1;
    A.a[0][0]=1;A.a[0][1]=0;A.a[0][2]=1;
    A.a[1][0]=2;A.a[1][1]=1;A.a[1][2]=2;
    A.a[2][0]=1;A.a[2][1]=1;A.a[2][2]=2;
    B.a[0][0]=1;B.a[0][1]=0;B.a[0][2]=0;
    B.a[1][0]=2;B.a[1][1]=1;B.a[1][2]=0;
    B.a[2][0]=1;B.a[2][1]=1;B.a[2][2]=1;
    scanf("%d%d",&n,&m);
    rei pre=-1;
    for(rei i=1,v;i<=m;++i){
        scanf("%d",&v);
        rei stp=v-pre-1;
        Matrix z=A;
        for(;stp;stp>>=1,z=z*z) if(stp&1) ans=z*ans;
        ans=B*ans;
        pre=v;
    }
    rei stp=n-pre-1;
    Matrix z=A;
    for(;stp;stp>>=1,z=z*z) if(stp&1) ans=z*ans;
    printf("%d\n",ans.a[2][0]);
    getchar(),getchar();
    return 0;
}

F

给定一个有 $n$ 个二元组的数组 $(A,B)$ ，数组 $C$ 包含 $n+1$ 个正整数，有 $q$ 个独立操作，每次向 $(A,B)$ 中加入一个二元组，需要：对 $(A,B)$ 中每个二元组选定一个元素 $L_i$ 为该二元组的值，将 $L,C$ 中的数两两匹配，当 $L$ 能匹配 $C$ 当且仅当 $L_i\leq C_i$ ，若成功，获得的分数为第 $1$ 步中取 $A$ 作为值的二元组的数量，对于每个操作，操作后给出最大可能分数，无解 $-1$

神仙贪心题qwq

为偷懒，将范围从 $1\sim n+1$ 扩展至 $0\sim n$

由于只需要大小关系，考虑将 $C$ 离散化，假设 $C_i=i-1$ ，考虑 $L$ 是否能与 $0\sim n$ 匹配

一个显然的贪心是：排序后若始终有 $L_i\leq i$ 则成立，把匹配看成括号序列，将 $L_i$ 看成左括号权值 $1$， $i$ 看成右括号权值 $-1$ ，合法序列为前缀和处处非负

可以把 $L_i$ 看成对区间 $[L_i,n)$ 的所有数 $+1$ ，即正覆盖 ；$i$ 对区间 $[i,n)$ 所有数 $-1$ ，即负覆盖

先考虑只有一种情况

对于二元组 $(A_i,B_i)$ 保证 $B_i\leq A_i$

先固定 $L_i=A_i$ ，做正覆盖，而最终的数中若还有负的，就需要最若干次 $[B_i,A_i)$ 的正覆盖来保证合法

问题转化为：

给定长度为 $n(0\sim n-1)$ 的序列 ，有 $n$ 个区间 $[B_i,A_i)$ 需要做尽可能少的正覆盖使所有数非负，求这个最小值

从左到右考虑每个 $x_i<0$ ， 设已经完成 $1\sim i-1$ 的部分，即，不需关心区间的左端点，有贪心：每次选择当前能覆盖 $i$ ，右端点最右的区间进行正覆盖直到 $x_i\geq 0$ ，正确性显然

考虑用堆来维护右端点，$0\sim n-1$ 枚举左端点 $i$ ，填入可行的右端点，不断选择最右的区间覆盖

若最终仍有负数则无解，否则用 $n$ 减去’额外的正覆盖次数’就是答案

再考虑如何处理多组询问

对于加入的数组 $(D,E)$ ，称补给正覆盖为其对原数组的影响

对于询问的数对，枚举其使用的时左/右侧元素以避免动态覆盖

对于询问的数对，选择正覆盖区间 $[\lambda,n)$ ，会转化为原序列中令 $x_\lambda,…,x_{n-1}$ 都 $+1$ 后的原问题

显然，$\lambda$ 越小，正覆盖的次数就越小，即这个区间只能靠补给正覆盖，即原来的区间正覆盖无法使 $x_i$ 非负

覆盖完后设 $i$ 是最小的满足 $x’_i=-1$ ，则显然必须有 $\lambda\leq i$

先前的正覆盖从左至右进行，现在需要从右至左考虑是否能删去一些正覆盖，仅考虑 $i$ 位置做过正覆盖时

  • 最终 $x’_i=0$

    此时 $[i,n]$ 存在补给正覆盖

    每个位置至多去掉一个，只考虑右端点 $r$ 最小(即1最后一次覆盖)的区间能否删去

    即，判断 $[i,r)$ 是否有 $0$ 的地方：

    • $x_i’=-1$ ，在补给正覆盖后 $x_i’=0$
    • 枚举到 $i_0$ 时区间被删去一个，从而 $x_{i_0}’=0$

    所以枚举当前 $x_i’=0$ 的最左位置，与 $r$ 比较，若删除成功更新最左位置

  • 最终 $x_i=-1$

    仅更新最左位置

对于每个 $\lambda \in [0,n)$ 求出补给正覆盖为 $[\lambda,n)$ 时额外正覆盖次数最小值 $ans_{\lambda}$

对每个询问 $(D_i,E_i)$ 答案就是 $n-\min\{ans_D,ans_E\}$

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
const int N=1e5+100;
const int INF=0x3f3f3f3f;
int n,Q;
int c[N],C[N],x[N],last[N],ans[N];
int cur=0,cov=0;
bool flag=false;
PII a[N];
priority_queue<int> q;

inline void down(int &x,const int y){ x>y ? x=y : 0;}
inline int pos(int val){ return lower_bound(x,x+n,val)-x;}

int main(){
    scanf("%d",&n),++n;
    for(rei i=1;i<n;++i) scanf("%d%d",&a[i].first,&a[i].second);
    for(rei i=0;i<n;++i) scanf("%d",&x[i]);
    sort(x,x+n);
    for(rei i=1;i<n;++i) down(a[i].second=pos(a[i].second),a[i].first=pos(a[i].first));
    fill(c,c+n,-1);
    for(rei i=1;i<n;++i) ++c[a[i].first],swap(a[i].first,a[i].second);
    sort(a+1,a+n);
    for(rei j=1,i=0;i<n;++i){
        for(cur+=c[i];j<n && a[j].first==i;++j) q.emplace(a[j].second);
        rei r=INF;
        while(q.size() && q.top()>i && cur<0){
            r=q.top(); q.pop();
            ++cur,++cov; --c[r];
        }
        while(q.size() && q.top()<=i) q.pop();
        C[i]=cur,last[i]=r;
        if(cur < -1){ flag=true; break;}
    }
    scanf("%d",&Q);
    if(flag){ for(;Q;--Q) puts("-1"); return 0;}
    rei j;
    for(rei r=n-1,i=n-1;i>=0;--i) ~C[i] ? last[i]<=r&&(r=i,--cov) : (r=j=i) ,ans[i]=cov;
    memset(ans+(j+1),63,(n-j+5)<<2);
    while(Q--){
        rei d,e,MIN;
        scanf("%d%d",&d,&e),MIN=min(ans[ pos(d) ],ans[ pos(e) ]+1);
        printf("%d\n",MIN>=INF ? -1 : n-MIN);
    }
    getchar(),getchar();
    return 0;
}