C
定义一个好字符串 $x$ 满足:$x=yy$ ,给出 $n$ , 求一个串 $s$ 满足 $|s|\leq 200$ ,且每个字符用 $[1,100]$ 的整数表示,且在 $s$ 的所有 $2^{|s|}$ 哥子序列中,恰好有 $n$ 个串是好的
有一个巧妙的构造方案:
分成前后两部分,后半部分为 $1\sim 100$ ,前半部分为 $1$ 至 $x \ (x\leq 100)$ ,好序列的个数为前半部分上升子序列的个数
从小到大增加前半部分的字符,放到最前面使方案数 $+1$ ,最后面使方案数 $\times 2$ ,而反向过来就是一个二进制拆分过程
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
| const int N=210;
int p[N],q[N],cnt;
ll n;
void solve(ll n){
if(!n) return ;
if(~n&1) q[ ++q[0] ]=cnt++,solve(n-1);
else p[ ++p[0] ]=cnt++,solve(n>>1);
}
int main(){
scanf("%lld",&n);
solve(n); printf("%d\n",cnt+100);
for(rei i=1;i<=q[0];++i) printf("%d ",cnt-q[i]);
for(rei i=p[0];i;--i) printf("%d ",cnt-p[i]);
for(rei i=1;i<=100;++i) printf("%d ",i);
getchar(),getchar();
return 0;
}
|
D
$n$ 个球,第 $i$ 个颜色为 $c_i$ ,质量为 $w_i$ ,有两种操作:选择两个同色且质量和不超过 $x$ 的球并交换位置 ; 选择两个异色且质量和不超过 $Y$ 的球并交换位置
求一共能得到多少不同的颜色序列
对于一种颜色,设所有球质量分别为 $w_1,w_2…w_n$ ,假设 $w_1<w_2<w_n$ ,易得若 $w_1+w_n\leq x$ 则这 $n$ 个球可以任意交换位置(以 $1$ 号球为媒介依次交换 $(1,i),(1,j),(i,1)$
若 $w_1+w_n>x$ 再设 $m$ 为最大的满足 $w_1+w_m\leq x$ 的数,考虑处理 $w_m\sim w_n$
考虑使用全局最小值,指与 $w_i$ 不同颜色的最小值,设为 $w_g$ ,对于要处理的部分,若 $w_g+w_i\leq y$ ,则 $(i,g)$ 可以互换位置(同样以 $1$ 为媒介),也就是数,满足 $w_g+w_i\leq y$ 的 $i$ 与 $1\leq i\leq m$ 的 $i$ 性质一样
但若 $w_g+w_i>y$ 则该球不能移动
对于剩下的球,将每种颜色视为整体,质量为所有球的总质量,可以发现其性质与小球一样
答案就是前 $m$ 种颜色的所有球的排列总数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
| const int N=2e5+100;
const int mod=1e9+7,INF=0x3f3f3f3f;
int n,S,D;
int fac[N],facinv[N];
ll ans=1;
int m,MIN=INF,sec=INF;
vector<int> s[N];
inline void down(int &x,const int y){ x>y ? x=y : 0;}
inline ll qpow(ll x,int y){ ll ans=1; while(y){ if(y&1) ans=ans*x%mod; x=x*x%mod; y>>=1;} return ans;}
inline void init(){
fac[0]=1;
for(rei i=1;i<=n;++i) fac[i]=(ll) fac[i-1]*i%mod;
facinv[n]=qpow(fac[n],mod-2);
for(rei i=n;i;--i) facinv[i-1]=(ll) facinv[i]*i%mod;
}
int main(){
scanf("%d%d%d",&n,&S,&D); init();
for(rei i=1,c,v;i<=n;++i) scanf("%d%d",&c,&v),s[c].emplace_back(v);
for(rei i=1;i<=n;++i) if(s[i].size()){
iter_swap(s[i].begin(),min_element(s[i].begin(),s[i].end()));
if(s[i].front()<MIN) sec=MIN,MIN=s[i].front();
else down(sec,s[i].front());
}
for(rei i=1;i<=n;++i) if(s[i].size() && s[i].front()+MIN<=D){
rei c=0,v=s[i].front()==MIN ? sec : MIN;
for(int u:s[i]) c+=u+s[i].front()<=S || u+v<=D;
m+=c,ans=ans*facinv[c]%mod;
}
printf("%d\n",ans*fac[m]%mod);
getchar(),getchar();
return 0;
}
|
E
数轴上有 $n(n\leq 2\times 10^5)$ 个绿洲,有一只储水量 $V(V\leq 2\times 10^5)$ 的骆驼,骆驼有两个操作:走到距离 $V$ 以内的一个绿洲;跳到任意绿洲,代价是 $V$ 会变为 $\left\lfloor \frac{V}{2} \right\rfloor$ ,注意当 $V=0$ 时不能跳,骆驼会从每个绿洲出发,对每一个判断能否一次性遍历所有绿洲
对于 $V,\frac{V}{2},\frac{V}{4},…$ 可以先预处理出此时那些绿洲之间可以直接走
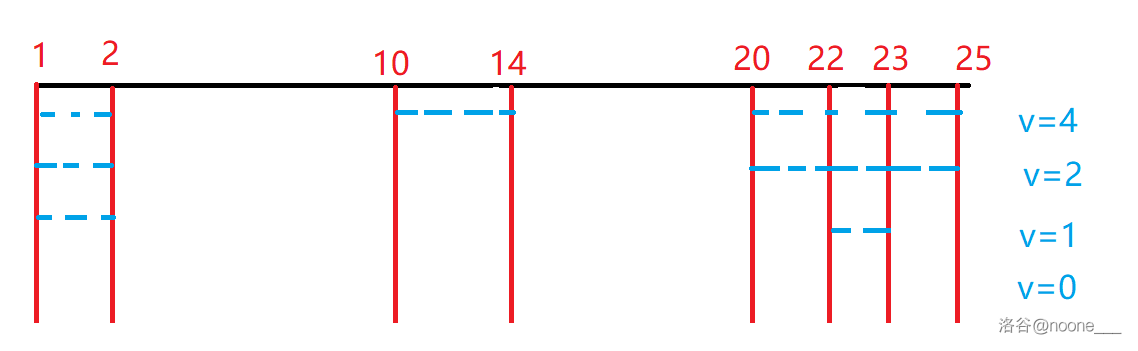
每跳一次相当于向下走一层,题目转化为钦定第一条线段,然后从每一层选一条,问是否能覆盖整个区间
神仙状压
设状态 $s$ 的第 $i$ 位为 $1$ 表示从第 $i$ 层选出一条线段, $f_1[s]$ 表示状态 $s$ 时从 $1$ 向右最多能延伸到的位置,$f_2[s]$ 表示状态 $s$ 时从 $n$ 向左做多能延伸到的位置
有转移:
即,从 $s_0$ 加上一条线段能延伸到的位置
检查答案时,对第一层的每一条线段寻找是否有 $s$ 使 $f_1[s],f_2[U-s-1]$ 贺该线段覆盖整个区间。用状态 $s$ 的线段尽可能扩展左半部分,剩下的线段(不包括第一层的)尽可能扩展右半部分
最多会跳 $\log {V+1}$ 所以全集的状态 $U=2^{\log {V+1}}-1$ 所以要开到 $2^{19}$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
| const int N=2e5+10,S=1<<19;
int n,V;
ll d[N];
int logV,a[25][N],U,f1[S],f2[S];
inline int upFind(int *a,int x){
rei L=1,R=a[0];
while(L<R-1){
rei mid=L+R>>1;
a[mid]<=x ? L=mid+1 : R=mid;
}
return a[L]>x ? a[L] : a[R];
}
inline int lowFind(int *a,int x){
rei L=1,R=a[0];
while(L<R-1){
rei mid=L+R>>1;
a[mid]<x ? L=mid : R=mid-1;
}
return a[R]<x ? a[R]+1 : a[L]+1;
}
int main(){
scanf("%d%d",&n,&V);
while((1<<logV)<=V) ++logV; ++logV;
for(rei i=1;i<=n;++i) scanf("%lld",&d[i]),d[i-1]=d[i]-d[i-1]; d[n]=0;
for(rei i=1;i<=logV;++i){
a[i][0]=1;
for(rei j=1;j<=n;++j){
a[i][ a[i][0] ]=j;
if(d[j]>(V>>(i-1))) ++a[i][0];
}
}
if(a[1][0]>logV){
for(rei i=1;i<=n;++i) puts("Impossible");
getchar(),getchar();
return 0;
}
U=(1<<logV)-1;
for(rei s=0;s<=U;++s) f1[s]=0,f2[s]=n+1;
for(rei s=0;s<=U;s+=2)
for(rei i=2;i<=logV;++i){
rei s0=1<<(i-1);
if(s&s0) continue;
f1[s|s0]=max(f1[s|s0],upFind(a[i],f1[s]));
f2[s|s0]=min(f2[s|s0],lowFind(a[i],f2[s]-1));
}
for(rei i=1;i<=a[1][0];++i){
bool flag=false;
rei fr=a[1][i-1]+1,to=a[1][i];
if(i==1) fr=1;
for(rei s=0;s<=U&&!flag;s+=2) if(fr<=f1[s]+1 && f2[U-s-1]-1<=to) flag=true;
if(flag) for(rei j=fr;j<=to;++j) puts("Possible");
else for(rei j=fr;j<=to;++j) puts("Impossible");
}
getchar(),getchar();
return 0;
}
|
F
给定长度为 $2n-1 \ (n\leq 60)$ 的数组 $a$ ,可以重排 $a$ 中的元素,再生成一个长度为 $n$ 的数组 $b$ ,其中 $b_i$ 是 $a_1\sim a_{2\times i-1}$ 的中位数,对于给定的 $a$ 球能生成多少种 $b$ ,对 $998244353$ 取模
神仙 $\text{dp}$ qwq
可以设 $a_i$ 升序,那么 $b_i$ 有两条性质:
- $b_i\in \{a_i,a_{i+1},…,a_n,…,a_{2n-i}\}$
- 不存在 $i<j$ 使 $b_i$ 介于 $b_j,b_{j+1}$ 之间
设 $f_{i,j,k}$ 表示当前确定了 $b_i\sim b_n$ 且第 $i$ 层左边还有 $j$ 个不同的数可供选择,右边还有 $k$ 个不同的数可供选择(不含 $b_i$ ),边界为 $f_{n,0,0}=1$
考虑转移:
- 若 $b_{i-1}=b_i$ 则两侧可供选择的数的个数不变,只需加上两侧新增的数 ($le$ 表示 $a_i$ 是否等于 $a_{i-1}$ ,$re$ 同理): $f_{i-1,j+le,k+re}\leftarrow f_{i,j,k}$
- 若 $b_{i-1}<b_i$ 由性质 $2$ 得之前的 $b_j$ 不能在范围 $(b_{i-1},b_i)$ 之间,那么这些数无用。则右侧可选的数多 $1$ ,左侧可选的数数量在 $0\sim j+le-1$ 任取: $f_{i-1,v,k+1+re}\leftarrow f_{i,j,k} \ \ \ \ (v\in [0,j+le])$
答案为当 $i=1$ ,任取 $j,k\in[0,2\times n-1]$ 求和
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
| const int N=125;
const int mod=1e9+7;
int n,G,ans;
int a[N],f[2][N][N],(*cur)[N]=*f,(*Next)[N]=f[1];
inline void fix(int &x){ x>=mod ? x-=mod : 0;}
int main(){
scanf("%d",&n); G=(n<<1)-1;
for(rei i=1;i<=G;++i) scanf("%d",&a[i]);
sort(a+1,a+1+G);
Next[0][0]=1;
for(rei i=n;i>1;--i){
swap(cur,Next); memset(Next,0,sizeof *f);
rei le=a[i]!=a[i-1],re=a[G-i+1]!=a[G-i+2];
for(rei j=0;j<=n-i<<1;++j)
for(rei k=0;k<=n-i<<1;++k){
rei c=cur[j][k]; if(!c) continue;
fix(Next[j+le][k+re]+=c);
for(rei v=0;v<j+le;++v) fix(Next[v][k+1+re]+=c);
for(rei v=0;v<k+re;++v) fix(Next[j+1+le][v]+=c);
}
}
for(rei i=0;i<=G;++i) for(rei j=0;j<=G;++j) fix(ans+=Next[i][j]);
printf("%d\n",ans);
getchar(),getchar();
return 0;
}
|
