E
给定长度为 $n$ 的序列 $a$ ,求有多少长度为 $n$ 的排列 $p$ 满足 $\forall i : p_i=a_i 或 p_{p_i}=a_i$
对于排列 $p$ ,将 $i$ 向 $p_i$ 连边,显然每个点入度出度都为 $1$ ,即,形成了若干个环
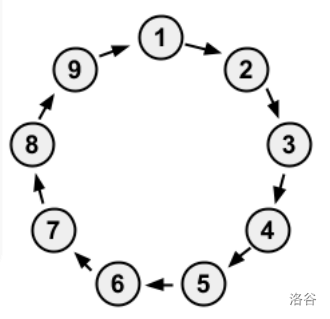
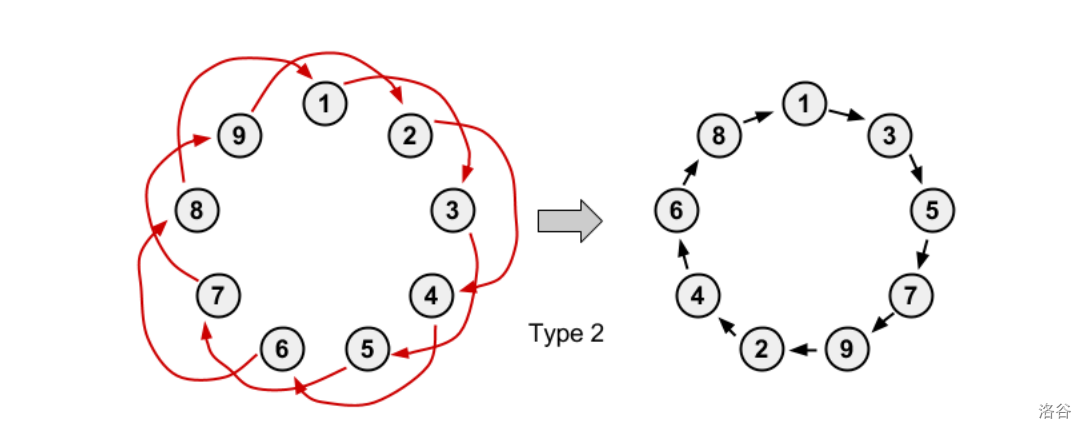
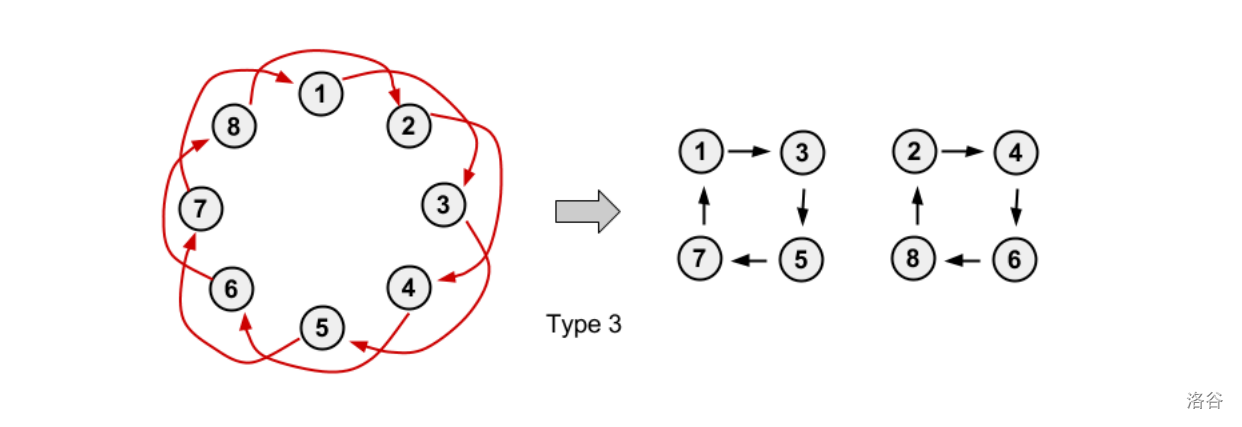
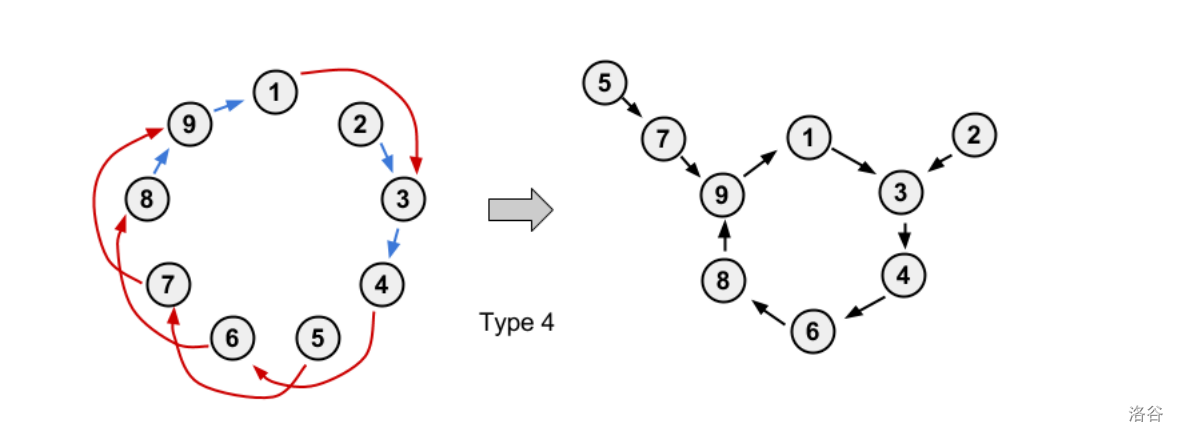
对于其中的一个环:删除所有边并将 $i\rightarrow a_i$ ,由题得 $a_i$ 是其前面的点( $p_i=a_i$ )或前面的前面的点( $p_{p_i}=a_i$ )
分成 $3$ ( $4$ )种:
现在有 $a$ 构成的图,反向考虑
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
| const int N=1e5+100;
const int mod=1e9+7;
int n,ans;
int a[N],du[N],cir[N],vis[N],chain_len[N],sum[N],f[N];
inline void fix(int &x){ x>=mod ? x-=mod : 0;}
void deal_cirtree(int x){
int now=0,fir_ch=0,la_ch=0,fir_len=0;
while(cir[x]){
++now,cir[x]=0;
if(chain_len[x]){
if(!fir_ch) la_ch=fir_ch=now,fir_len=chain_len[x];
else{
int kl=(chain_len[x]<now-la_ch)+(chain_len[x]<=now-la_ch);
ans=(ll) ans*kl%mod,la_ch=now;
}
}
x=a[x];
}
if(!fir_ch) ++sum[now];
else{
int kl=(fir_len<now-la_ch+fir_ch)+(fir_len<=now-la_ch+fir_ch);
ans=(ll) ans*kl%mod;
}
}
void work(){
for(rei i=1;i<=n;++i){
if(du[i]) continue;
int x=i,len=0; while(!cir[x]) x=a[x],++len;
chain_len[x]=len;
}
ans=1;
for(rei i=1;i<=n;++i) if(cir[i]) deal_cirtree(i);
for(rei i=1;i<=n;++i){
if(!sum[i]) continue;
f[0]=1;
for(rei j=1;j<=sum[i];++j){
if(i>1 && (i&1)) fix(f[j]=f[j-1]+f[j-1]);
else f[j]=f[j-1];
if(j>1) fix(f[j]+=(ll) f[j-2]*(j-1)%mod*i%mod);
}
ans=(ll) ans*f[sum[i]]%mod;
}
}
int main(){
scanf("%d",&n);
for(rei i=1;i<=n;++i) scanf("%d",&a[i]),++du[ a[i] ];
for(rei i=1;i<=n;++i){
if(vis[i]) continue;
rei x=i; while(!vis[x]) vis[x]=i,x=a[x];
if(vis[x]!=i) continue;
while(!cir[x]) cir[x]=1,x=a[x];
}
for(rei i=1;i<=n;++i) if((cir[i] && du[i]>2) || (!cir[i] && du[i]>1)) return puts("0"),0;
work();
printf("%d\n",ans);
getchar(),getchar();
return 0;
}
|
F
给定 $n$ 个点的树,每条边长度为 $1$ 给定 $S$ 表示喜欢的顶点集合,起初所有点为白色,可以做一次操作,其中选择顶v点 $\in S$ 和整数 $d$ 将所有满足 $dis(v,u)\leq d$ 的点 $u$ 染成黑色,求最终能得到多少形态不同的树
先考虑 $S$ 为全集,即每个点都能以其自身为中心操作,那么最终黑色的点形成一个连通块
注意到不同操作方案可能得出同一种连通块,即,这并不是一一对应的
考虑到操作有一定距离且连通块是树,考虑取直径中点,即,对于每个连通块,看成以其中心为操作中心的操作,同时得到尽可能小的 $d$
当中心是边时,显然一侧为子树,规定以该边靠近叶子的点作为操作中心
而对于整棵树并不计入,仅在最后将答案 $+1$
对于每个顶点 $v$ ,考虑以其为操作中心的操作个数,对于全集 $S$ ,一定有 $d\in [0,sup]$
而对 $d$ 的约束有:
- $d<f_v$ ,即, $d$ 小于整棵树的深度,以防整棵树被染黑
- $d\leq g_v-1$ ,即,$d$ 小于以 $child(v)$ 中点为根的所有子树中第二大深度为 $g_v$ 的 : 即考虑 $v$ 不是中心的情况,若中心在某子树中,朝根方向走,黑色点的最大深度严格递减,即 $\forall c\in child(v)$ 必须有 $\{u\mid dis(c,u)\leq d-1\}\not =\{u\mid (v,u)\leq d\}$ ,即,至少需要两颗子树存在深度 $\geq d-1$ 的顶点
即,$d\leq \min(f_v-1,g_v+1)$ ,对于其余的 $v$ ,换根 $\text{dp}$ 即可
再考虑 $S$ 不是全集,此时 $d$ 要考虑下界
以 $v$ 为操作中心的一些操作可以被 以 $u\in child(v)$ 为中心的操作 $(u,d’)$ 代替,则 $d’\geq d+dis(v,u)>d$
则,子树 $subtree(u)$ 中不能存在深度 $\geq d$ 的顶点,即,操作 $(v,d)$ 至少覆盖了它的一个子节点的子树 $subtree(u)$
这说明 $d$ 至少大于其所有子树中深度最大值的最小值,且保证子树中至少有一个 $S$ 中的点,否则 $v$ 不存在
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
| const int N=2e5+100;
int n;
int head[N],ver[N<<1],Next[N<<1],tot;
int fa[N],Size[N],f[N],g[N],inf[N];
char s[N];
ll ans=1;
inline void up(int &x,const int y){ x<y ? x=y : 0;}
inline void down(int &x,const int y){ x>y ? x=y : 0;}
inline void add(int u,int v){ ver[++tot]=v,Next[tot]=head[u],head[u]=tot;}
void dfs1(int x){
Size[x]=s[x]&=1;
inf[x]=(s[x]-1)&INT_MAX;
for(rei i=head[x];i;i=Next[i]){
rei y=ver[i]; if(y==fa[x]) continue;
fa[y]=x; dfs1(y); Size[x]+=Size[y];
f[x]<=f[y] ? (g[x]=f[x],f[x]=f[y]+1) : (up(g[x],f[y]+1),0);
if(Size[y]) down(inf[x],f[y]+1);
}
}
void dfs2(int x,int fy=-1){
rei sup;
f[x]<=fy ? (g[x]=f[x],f[x]=fy+1) : (up(g[x],fy+1),0);
if(Size[x]<Size[1]) down(inf[x],fy+1);
if(inf[x]<=(sup=min(f[x]-1,g[x]+1))) ans+=sup-inf[x]+1;
for(rei i=head[x];i;i=Next[i]){
rei y=ver[i]; if(fa[y]!=x) continue;
dfs2(y,f[y]+1==f[x] ? g[x] : f[x]);
}
}
int main(){
scanf("%d",&n);
for(rei i=1,u,v;i<n;++i) scanf("%d%d",&u,&v),add(u,v),add(v,u);
scanf("%s",s+1);
dfs1(1),dfs2(1);
printf("%lld\n",ans);
getchar(),getchar();
return 0;
}
|