noone___'s blog
0%

60801202-AGC004

发表于 更新于 分类于
AGC004

这场好难qwq 我好菜

B

有 $2$ 种操作: 花费 $a_i$ 秒，直接获得颜色 $i$ 和 花费 $x$ 秒，使得之前获得的颜色 $i$ 全部变为颜色 $(i+1) \ \text{mod} \ n$ ，求收集到 $0$ 到 $n-1$ 所有颜色的最短时间

每种方案的 $2操作$ 取决于被 $2操作$ 作用次数最多的颜色，考虑枚举 $2操作$ ，滑动窗口查询最小值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
const int N=4e3+100;
int n,x,a[N],q[N];
ll ans;

int main(){
    scanf("%d%d",&n,&x);
    for(rei i=1;i<=n;++i) scanf("%d",&a[i]),a[i+n]=a[i];
    for(rei k=0;k<n;++k){
        ll s=(ll) k*x; rei l=1,r=0;
        for(rei i=1;i<=k;++i){
            while(l<=r && a[ q[r] ]>=a[i]) --r;
            q[++r]=i;
        }
        for(rei i=k+1;i<=n+k;++i){
            while(l<=r && i-k>q[l]) ++l;
            while(l<=r && a[ q[r] ]>=a[i]) --r;
            q[++r]=i; s+=a[ q[l] ];
        }
        ans=k ? min(ans,s) : s;
    }
    printf("%lld\n",ans);
    getchar(),getchar();
    return 0;
}

C

给出一个由 # 和 $.$ 组成的矩阵，让你给出两个大小相同且 # 是相连的矩阵，且这两个矩阵的 $.$ 重叠部分刚好是给出的这个矩阵。

考虑题目中保证边界不被染色，即边界中不含有 $.$

所以只需要让行按照奇偶染色，最后一边染起始列，一边染结束列来保证连通

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
const int N=510;
int n,m;
char s[N][N],a[N][N],b[N][N];

int main(){
    scanf("%d%d",&n,&m);
    for(rei i=1;i<=n;++i) scanf("%s",s[i]+1);
    for(rei i=1;i<=n;++i) for(rei j=1;j<=m;++j) a[i][j]=b[i][j]=s[i][j];
    for(rei i=1;i<=n;++i) a[i][1]=b[i][m]='#';
    for(rei i=1;i<=n;++i) for(rei j=2;j<m;++j) i&1 ? a[i][j]='#' : b[i][j]='#';
    for(rei i=1;i<=n;++i) printf("%s\n",a[i]+1);
    puts("");
    for(rei i=1;i<=n;++i) printf("%s\n",b[i]+1);
    getchar(),getchar();
    return 0;
}

D

$n$ 个城市，每个城市有一个传送点，传送到唯一另外一个城市，保证经过多次传送始终能到达 $1$ 号城市。现在修改一些点的目的地，使得从任何一点出发在传送 $k$ 次之后恰好都能到达 $1$ 号城市，求最少改变的数量。

简化问题模型：城市构成一个基环内向树，要求修改尽可能少的出边是每个点到 $1$ 号点需要经过至多 $k$ 条边（考虑到没说禁止自环

那么选一些点传送至 $1$ 号点，再把原树分为几颗，其中最大深度不能超过 $k-1$，贪心即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
const int N=1e5+100;
int tot,head[N],Next[N<<1],ver[N<<1];
int n,m;
int ac[20][N],d[N],cov[N],ans,fa[N];
priority_queue<PII> q;

inline void add(int u,int v){ ver[++tot]=v,Next[tot]=head[u],head[u]=tot;}
void dfs(int x){
    d[x]=d[ fa[x] ]+1;
    for(rei i=1;i<20;++i) ac[i][x]=ac[i-1][ ac[i-1][x] ];
    for(rei i=head[x];i;i=Next[i]) dfs(ver[i]);
}

void cover(int x){
    if(cov[x]) return; cov[x]=1;
    for(rei i=head[x];i;i=Next[i]) cover(ver[i]);
}

int main(){
    scanf("%d%d",&n,&m);
    for(rei i=1;i<=n;++i) scanf("%d",&fa[i]);
    for(rei i=2;i<=n;++i) add(ac[0][i]=fa[i],i);
    ans+=fa[1]!=1;//添加1节点的自环
    dfs(1);
    for(rei i=1;i<=n;++i) q.push(mk(d[i],i));
    while(q.size()){
        rei x=q.top().second,anc=x; q.pop();
        if(cov[x] || d[x]-d[1]<=m) continue;
        for(rei i=19;~i;--i) if(d[x]-d[ ac[i][anc] ]<m && ac[i][anc]) anc=ac[i][anc];
        cover(anc); ++ans;
    }
    printf("%d\n", ans);
    getchar(),getchar();
    return 0;
}

E

一个棋盘，每个格子有机器人或空格或出口 ，每次命令所有机器人向任意一个方向移动一格，如果超出了棋盘的边界或到了出口就会消失，求机器人到出口的最多数量

让机器人移动相当于移动出口，出口自带框，出框的机器人消失，出口抵达的机器人出去

定义 $l,r,u,d$ 四个参数表示出口 $E$ 向 $4$ 个方向能抵达的最远位置，在最优情况下出口会跑成一个矩形

官方图1

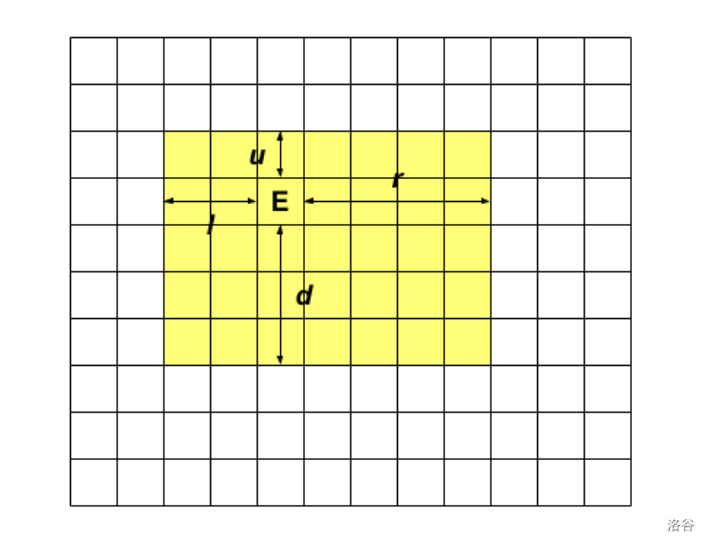
黄色区域就是机器人的移动范围，在该范围内的机器人取舍已经被计算好

再考虑曾经有这个移动范围时，不能走的格子

官方图2

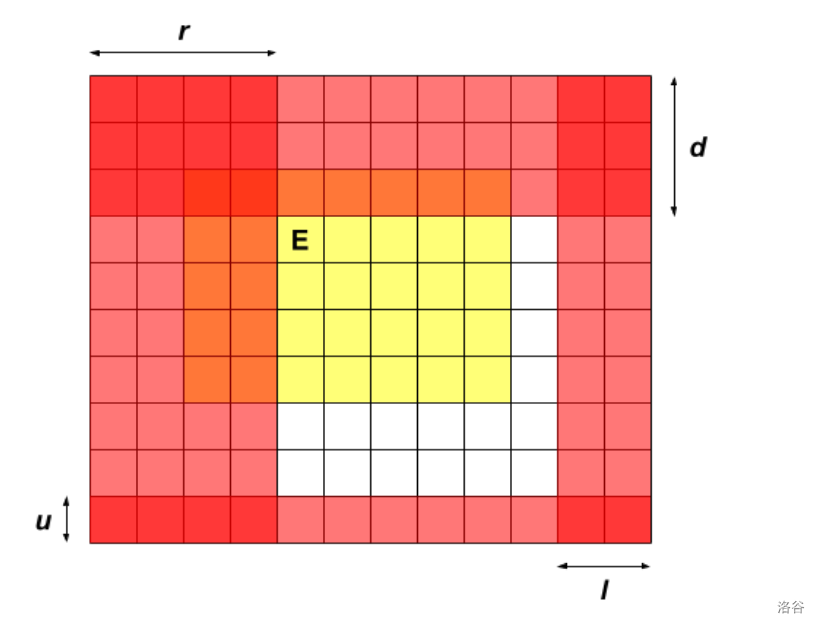
纯红色区域中的机器人全部死亡，不管

对于红黄详见的部分之前已经取舍，考虑白色部分的转移：

官方图3

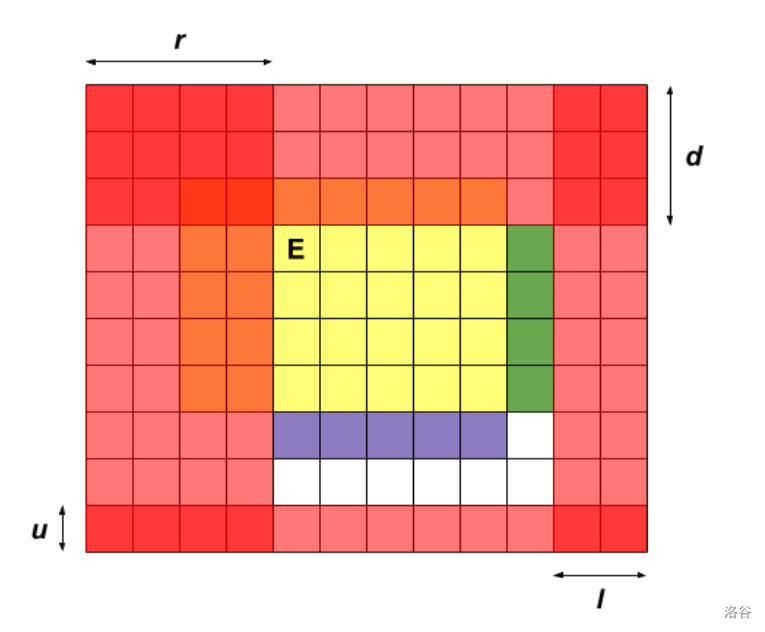
移动范围扩大，加上相应颜色区域的机器人数量即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
const int N=1e2+5;
inline int max(int a,int b){ return a>b?a:b;}
inline int min(int a,int b){ return a<b?a:b;}
short f[N][N][N][N],g[N][N],h[N][N];
char s[N][N];
int n,m,ans,px,py;

int main(){
    scanf("%d%d",&n,&m);
    memset(f,-1,sizeof f);
    for(rei i=1;i<=n;++i) scanf("%s",s[i]+1);
    for(rei i=1;i<=n;++i) for(rei j=1;j<=m;++j){
            if(s[i][j]=='E') px=i,py=j;
            g[i][j]=g[i][j-1]+(s[i][j]=='o');
            h[i][j]=h[i-1][j]+(s[i][j]=='o');
        }
    f[0][0][0][0]=0;
    rei pl=py-1,pr=m-py,pd=px-1,pu=n-px,p;
    for(rei l=0;l<=pl;++l) for(rei r=0;r<=pr;++r) for(rei d=0;d<=pd;++d) for(rei u=0;u<=pu;++u){
        if(!(~f[l][r][d][u])) continue;
        rei cl=max(r+1,py-l),cr=min(m-l,py+r),cd=max(u+1,px-d),cu=min(n-d,px+u);
        if((p=py+r+1)<=m-l) f[l][r+1][d][u]=max(f[l][r+1][d][u] , f[l][r][d][u]+h[cu][p]-h[cd-1][p]);
        if((p=py-l-1)>=r+1) f[l+1][r][d][u]=max(f[l+1][r][d][u] , f[l][r][d][u]+h[cu][p]-h[cd-1][p]);
        if((p=px+u+1)<=n-d) f[l][r][d][u+1]=max(f[l][r][d][u+1] , f[l][r][d][u]+g[p][cr]-g[p][cl-1]);
        if((p=px-d-1)>=u+1) f[l][r][d+1][u]=max(f[l][r][d+1][u] , f[l][r][d][u]+g[p][cr]-g[p][cl-1]);
        ans=max(ans,f[l][r][d][u]);
    }
    printf("%d\n",ans);
    getchar(),getchar();
    return 0;
}

F

给定一个 $N$ 个点，$M$ 条边的连通无向简单图，其中 $N_1\leq M\leq N$ ，每个点可以为黑或白，初始每个点都白。每次选择一对具有相同颜色且相邻的顶点，并反转它们的颜色 (即如果一条边的两端是白色的，可以将其变为黑色)。询问是否存在一种方案，将所有的点都变成黑色，输出最少的操作次数。

由数据范围：

  • 先考虑树的情况

    把树看成一个二分图并将所有点重新染色-左红右蓝。如此在初始时所有边上的点颜色都不相同

    考虑每次操作：将颜色相同的点反色。转化为新染色方案中，找一对颜色不同的两端点，并交换颜色。显然有 \原图中两点颜色相同的边经过反色操作形成的反色且颜色相同的边** 对应到 \新的染色方案中两点颜色不同的边操作后两点颜色仍不同**

    所以问题转化为是否有方案将左红右蓝转化为左蓝右红

    在新染色方案上考虑，找到不变量红点数量与蓝点数量。显然若初始时 $num_红!=num_蓝$ 无解

    移动红点到原先蓝点的位置。 直接计算最少方案并不容易，考虑每条边的贡献

    设这条边断掉后，左边红点比蓝点多 $L$ 个，则改变一定还需要被经过 $L$ 次

    所以枚举每条边，统计出其一侧的红蓝点数量差并将绝对值相加

  • 基环树

    由于刚才用到二分图的性质，因此想到对基环树分奇环/偶环考虑

    • 奇环

      为满足二分图，先断掉这个奇环，此时问题与树的情况相同

      在考虑断掉的边，由于奇环，该边的两端点在二分图中处于同一侧

      所以该边的两个端点可以同时改变颜色，即 $2蓝\Rightarrow 2红$ 或 $2红\Rightarrow 2蓝$

      可以把红色看成棋子，蓝色看成空位。这条边相当于一个\源/汇**，可以不断提供/吞没成对的棋子

      $\therefore$ 这里判断的是红蓝色是否有相同的奇偶性，否 则无解，是 则算出源/汇需要提供多少次棋子，并与树情况算出的累加

    • 偶环

      对于偶环仍然满足二分图性质，所以需要判断的是红蓝点数是否相同

      偶环的作用是提供枢纽，减少环中绕行的次数。显然环外的边经过次数不变，而环内边的经过次数相互约束：环内相邻两条边的经过次数（带符号）的差值恒定且与点有关

      可以发现环上的交换是一个均分纸牌问题，求中位数即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
#define rei register int
#define ll long long
using namespace std;

const int N=100054;
int n,m,L;
int ver[N<<1],head[N],Next[N<<1],tot;
int fa[N],depth[N],Size[N];
int cnt,buf[N];
ll ans;

inline int ad(int x){ return (x-1^1)+1;}
inline void add(int u,int v){ ver[++tot]=v,Next[tot]=head[u],head[u]=tot; ver[++tot]=u,Next[tot]=head[v],head[v]=tot;}

void dfs(int x){
    Size[x]=-(depth[x]&1) | 1;
    for(rei i=head[x],y;i;i=Next[i])
        if(!~fa[ y=ver[i] ]) fa[y]=x,depth[y]=depth[x]+1,dfs(y),Size[x]+=Size[y];
        else if(depth[x]<depth[y]) L=i;
}

int main(){
    rei incr; scanf("%d%d",&n,&m);
    for(rei i=0,u,v;i<m;++i) scanf("%d%d",&u,&v),add(u,v);
    memset(fa,-1,sizeof fa),fa[1]=0;
    dfs(1);
    if(m==n-1){//树
        if(Size[1]) return puts("-1"),0;
        for(rei i=1;i<=n;++i) ans+=abs(Size[i]);
        return printf("%lld\n",ans),0;
    }
    rei	u=ver[ ad(L) ],v=ver[L];
    if( (depth[u]^depth[v]) &1){//偶环
        if(Size[1]) return puts("-1"),0;
        for(rei i=v;i!=u;i=fa[i]) buf[cnt++]=Size[i];
        ++cnt;
        nth_element(buf,buf+cnt/2,buf+cnt);
        for(rei i=0;i<cnt;++i) ans+=abs(buf[i]-buf[cnt/2])-abs(buf[i]);
    }
    else{//奇环
        if(Size[1]&1) return puts("-1"),0;
        incr=-Size[1]/2,ans=abs(incr);
        rei i;
        for(i=v;i!=u;i=fa[i]) Size[i]+=incr;
        for(;i;i=fa[i]) Size[i]+=incr<<1;//加上源/汇点贡献
    }
    for(rei i=1;i<=n;++i) ans+=abs(Size[i]);
    printf("%lld\n",ans);
    getchar(),getchar();
    return 0;
}