noone___'s blog
0%

矩阵树定理

发表于 更新于 分类于
咕了好久的矩阵树定理

前置芝士

行列式

行列式为标量，对于矩阵 $A$ 来说，其行列式定义为：

其中 $P$ 取遍 $1\sim n$ 的所有排列，$\delta(P)$ 取 $P$ 的逆序对数

即，对每一个矩阵每行每列只选择一个元素并求他们的乘积，其乘积相加减（取决于逆序对数）

对于 $n$ 阶行列式，有 $n!$ 项

  • eg:

  • 计算

    其中 $A’$ 是 $A$ 的上三角矩阵

高斯消元在 $O(n^3)$ 内求出 $n$ 阶矩阵的行列式

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
inline ld determinant(ld (*A)[N],int n){
    int s=1;
    for(rei i=1,c=1,j;i<=n;++i){
        for(j=c;j<=n && fabs(A[j][i])<eps;++j);
        if(j==n+1) continue;
        s-=s;
        for(rei k=1;k<=n;++k) swap(A[c][k],A[j][k]);
        for(j=c+1;j<=n;++j)
            if(fabs(A[j][i])>eps){
                ld t=A[j][i]/A[c][i];
                for(rei k=i;k<=n;++k) A[j][k]-=A[c][k]*t;
            }
        ++c;
    }
    ld ans=1;
    for(rei i=1;i<=n;++i) ans*=A[i][i];
    return fabs(ans);
}

$k$ 阶主子式

在 $n$ 阶行列式中，选取行数和列数都为 $i$ 个的行列式即为 $n$ 阶行列式的 $i$ 阶主子式

关联矩阵与邻接矩阵与基尔霍夫矩阵

对于无向图 $G=(V,E) V=\{v_1,v_2,…,v_n\},E=\{e_1,e_2,…,e_m\}$

邻接矩阵

设 $edgenum_{i,j}$ 表示顶点 $v_i,v_j$ 之间的边数，邻接矩阵即为：$A(G)=(edgenum_{i,j})_{n\times n}$ 的矩阵

  • $A(G)$ 为对称矩阵
  • 若 $G$ 为无环图，那么 $A(G)$ 中第 $i$ 行/列的元素之和等于 $deg_{v_i}$
  • 图 $G,H$ 同构的充要条件是存在置换矩阵 $P$ 使 $A(G)=P^TA(H)P$ 但这条并没有什么用
  • $eg：$
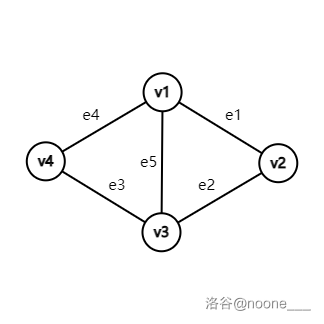    https://cdn.luogu.com.cn/upload/image_hosting/6quf8jfy.png 该无向图的邻接矩阵为 $\begin{bmatrix}0 & 1 & 1 & 1 \\ 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 \\ 1 & 0 & 1 & 0\end{bmatrix}$

关联矩阵

  • 设 $m_{i,j}$ 表示顶点 $v_i$ 与边 $e_j$ 关联的次数，$M(G)=(m_{ij})_{n\times m}$ 为图 $G$ 的关联矩阵

  • 类似的，对于有向图，关联矩阵的 $m_{i,j}$ 定义为

基尔霍夫矩阵

  • 定义基尔霍夫矩阵满足:

    其中 $e_{u,v}$ 表示若 $u,v$ 相连，则 $e(u,v)=1$

矩阵树定理及其扩展

矩阵树定理

一个无重边，自环的图 $G$ 的生成树个数，等于其基尔霍夫矩阵任意一个 $n-1$ 阶主子式的行列式的绝对值

变元矩阵树定理

对于生成树 $T$ 定义求其边权之积的函数：

那么有：

有向图的矩阵树定理

  • 对于外向树：

  • 对于内向树

其中，以 $i$ 为起点/终点的树形图数量为 去掉第 $i$ 列和第 $i$ 行形成的 $n-1$ 阶主子式的行列式的值

$D^I,D^O$ 分别为入度,出度矩阵，$A$ 是邻接矩阵

一个栗子

求 $n$ 个点组成的无根带标号树的个数，即，求无向完全图生成树计数

其基尔霍夫矩阵主对角线都是 $n-1$ ，其余均为 $-1$

让第一行加上其余行，第一行均为 $1$ ，第一行加上其余行，每行在主对角线上的为 $n$ ，其余为 $0$，最后变为一个上三角矩阵，行列式为主对角线元素相乘

$\therefore$ 是 $n^{n-2}$

例题

P3317 [SDOI2014]重建

给定一张无向完全图以及每条边没有被损毁的概率，求最后剩下的边正好组成原图的一颗生成树的概率

由题意易得，答案为：

尝试往变元矩阵树定理的形式上面靠，有：

1
2
3
4
for(rei i=1;i<=n;++i) for(rei j=1;j<=n;++j){ scanf("%lf",&G[i][j]); if(G[i][j]==1) G[i][j]-=eps;}
for(rei i=1;i<=n;++i) for(rei j=1;j<i;++j) res*=1-G[i][j];
for(rei i=1;i<=n;++i) for(rei j=1;j<=n;++j) if(i!=j) G[i][j]/=(1-G[i][j]),G[i][i]+=G[i][j],G[i][j]=-G[i][j];
printf("%.10lf\n",res*determinant(G,n-1));

P4208 [JSOI2008]最小生成树计数

给出一个简单无向加权图，求这个图中有多少不同的最小生成树

结论题：所有最小生成树中，边权相等的边数量相同，且删去这些边后，图连通性不变

给出草率的证明：

从 $\text{Kruskal}$ 的过程开始，吧加入相同权值的边看作一个阶段，每次加边加至图中会形成环为止，然后进行下一阶段。把之前已经被较小边权的边连通的连通块看作一个点，那么就是在这些点间随便连边。如果会形成环，可以选择不加入该边或者删去一条边并加入该边，对连通性和生成树中该种边权的边的条数没有影响

求最小生成树的个数，仍然把相同权值的比看成阶段，那么就是求每个阶段连边方案数的积，那么先求一次最小生成树，再跑一次 $\text{Kruskal}$ ，对于每个阶段，将原先最小生成树中除该阶段的边的其他边连进图中，并查集将图缩点，在缩点后的图中加入该阶段所有边，其实新图的生成树方案中每一种都对应原图中该阶段的一种加边方案，矩阵树定理求生成树即可

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
const int N=2e3+100;
const int mod=31011;
const double eps=1e-6;
bool used[N];
int fa[N],n,m;
int u[N],v[N],w[N],r[N],tot;
ld K[N][N];
int ind[N];

inline int find(int u){ return u==fa[u] ? u : fa[u]=find(fa[u]);}
inline void add(int _u,int _v,int _w){ u[++tot]=_u,v[tot]=_v,w[tot]=_w;}
inline bool cmp(const int a,const int b){ return w[a]<w[b];}

inline ld determinant(ld (*A)[N],int n){
    int s=1;
    for(rei i=1,c=1,j;i<=n;++i){
        for(j=c;j<=n && fabs(A[j][i])<eps;++j);
        if(j==n+1) continue;
        s-=s;
        for(rei k=1;k<=n;++k) swap(A[c][k],A[j][k]);
        for(j=c+1;j<=n;++j)
            if(fabs(A[j][i])>eps){
                ld t=A[j][i]/A[c][i];
                for(rei k=i;k<=n;++k) A[j][k]-=A[c][k]*t;
            }
        ++c;
    }
    ld ans=1;
    for(rei i=1;i<=n;++i) ans*=A[i][i];
    return fabs(ans);
}

namespace MST{
    inline void Add_edge(int idx){
        int x=ind[find(u[idx])],y=ind[find(v[idx])];
        ++K[x][x],++K[y][y];
        --K[x][y],--K[y][x];
    }
    inline void Kruskal(int n,int m){
        for(rei i=1;i<=n;++i) fa[i]=i;
        for(rei i=1;i<=m;++i) r[i]=i;
        sort(r+1,r+m+1,cmp);
        for(rei i=1;i<=m;++i){
            rei x=r[i];
            if(find(u[x])!=find(v[x])){
                fa[ find(u[x]) ]=find(v[x]);
                used[x]=true;
            }
        }
    }
    inline void merge(int idx){ if(find(u[idx])!=find(v[idx])) fa[ find(u[idx]) ]=find(v[idx]);}
    inline int Build_Graph(int n,int m,int L,int R){
        rei tot=0;
        for(rei i=1;i<=n;++i) for(rei j=1;j<=n;++j) K[i][j]=0;
        for(rei i=1;i<=n;++i) fa[i]=i;
        for(rei i=1;i<=m;++i) if(used[ r[i] ] && (i<L || i>R)) merge(r[i]);
        memset(ind,0,sizeof ind);
        for(rei i=1;i<=n;++i) if(!ind[ find(i) ]) ind[ find(i) ]=++tot;
        for(rei i=L;i<=R;++i) Add_edge(r[i]);
        return tot;
    }
    inline int Kruskal_cal(int n,int m){
        rei ans=1;
        for(rei L=1,R=1;R<=m;L=R){
            bool ok=false;
            while(w[ r[L] ]==w[ r[R] ] && R<=m) if(used[ r[R++] ]) ok=true;
            if(!ok) continue;
            rei tot=Build_Graph(n,m,L,R-1);
            ans=(ll) ans*(int) round(determinant(K,tot-1))%mod;
        }
        return ans;
    }
}

int main(){
    scanf("%d%d",&n,&m);
    for(rei i=1,uu,vv,ww;i<=m;++i) scanf("%d%d%d",&uu,&vv,&ww),add(uu,vv,ww);
    MST::Kruskal(n,m);
    printf("%d\n",MST::Kruskal_cal(n,m));
    getchar(),getchar();
    return 0;
}

best 定理

定理及证明

对于一个有向欧拉图，设点 $i$ 的出度为 $out_i$ ，那么其从点 $s$ 出发的欧拉回路个数为：

其中 $T_u (G)$ 为图 $G$ 以 $u$ 为根的内向生成树个数

式子的含义为：

除去点 $s$ ，每个点指定一条出边作为树边，$s$ 的所有出边任意指定一个顺序，除了 $s$ 的点，把其非树边出边任意指定顺序

如此得到的一个指定顺序的内向树与所有从 $s$ 出发的欧拉路径一一对应

整个有向图 $G$ 的欧拉回路数量为，随意指定一点 $s$ ：

谔谔，证明都被猫吃掉了 $\rightarrow$ (o=^•ェ•)o