CF1515E Phoenix and Computers
我们始终不知道EI是怎么写的
#include<bits/stdc++.h>
#define R(X,Y) X=(X+Y)%P;
int64_t g[410],n,P,k,a,f;int main(){std::cin>>n>>P;g[0]=f=k=1;for(--n;n>=0;n-=2,++k){for(int i=1;i<=n;++i)R(g[i],g[i-1]*k*2)f=f*k%P;R(a,g[n]*f)}printf("%d\n",a);}
</code></pre>
</details>
题意
要开启 $n$ 台电脑,若第 $i-1,i+1$ 台被开启,第 $i$ 台自动开,询问打开所有电脑的方案数
解
题解里有一个吊打标算的 $O(n^2)$ 做法
上面EI的代码好像也是 $O(n^2)$
设 $dp_{i,j}$ 表示已开机 $i$ 台,形成 $j$ 个连续段,每段距离 $>1$ 且不确定
考虑转移:
新建段
- $dp_{i+1,j+1}=\sum dp_{i,j}*(j+1)$ ,即在 $j+1$ 个间隔中选择一个打开
扩展段
- $dp_{i+1,j}=\sum dp_{i,j}\cdot j\cdot2$ ,即在一段的边界+1处开
- $dp_{i+2,j}=\sum dp_{i,j}\cdot j\cdot2$ ,即在一段的边界+2处开
合并段(仅当 $j\geq 2$ 时)
- $dp_{i+2,j-1}=\sum dp_{i,j}\cdot(j-1)\cdot2$ ,即当两边距离为 $2$ 时有两种开法
- $dp_{i+3,j-1}=\sum dp_{i,j}\cdot (j-1)$ ,即两边距离为 $3$ 时开中间
CF1516D Cut
题意
给定长度为 $n$ 的序列,$q$ 次询问,对于 $[l,r]$ 区间最少能分成多少个子序列满足,子序列中数的乘积等于它们的 $\text{lcm}$
解
很显然子序列中所有数互质,有贪心:从左往右尽可能多的选取直至会加入与原区间不互质的数
设 $Next_i$ 代表从 $i$ 开始的序列停止的位置,即向以 $i$ 开始的子序列中加入 $Next_i$ 会使序列中的数不再互质
$dp_{i,l}$ 表示从 $l$ 开始,跳 $Next_i$ $2^i$ 次到达的位置
CF1516E Baby Ehab Plays with Permutations
前置芝士
置换
简单来说是对一个序列进行重排列,
即 $[1,n]$ 到 $[1,n]$ 的一一映射
$1.$
置换可以分解为若干循环,具体为连边:$1\rightarrow a_1 \ ,\ 2\rightarrow a_2 \ ,\ \dotsb \ ,\ i\rightarrow a_i \ ,\ \dotsb \ ,\ n\rightarrow a_n$
形成的图中会有若干个环,即,置换可以被分解成不相交循环的积
一个循环可以被拆成 $环长-1$ 个对换,所以通过 $环长-1$ 步可以还原该循环
关于第一类斯特林数的计算
变形得
即
题意
给出长为 $n$ 的序列 $p$ 满足 $p_i=i$,进行 $k$ 次操作,每次可以选取序列中两个位置并交换,对于 $1\sim k$ 的每个值,输出最终可能有几个序列
解
$dp$ 方程难以表达,不能直接求出总排列数
反向思考,求经过 $k$ 次交换后恰好能排好序的排列数
由置换与群可知,若该排列 $p$ 中有 $c$ 个循环,需要 $n-c$ 步来还原
$\therefore$ 需要 $k$ 来还原的排列中存在 $n-k$ 个循环
由第一类斯特林数定义可知,满足条件的排列数就是 $\begin{bmatrix}n \\ n-k\end{bmatrix}$
$\therefore$ 对于 $1\sim k$ 的询问,答案依次为
然而由于递推求斯特林数 $O(n^2)$,由于 $k\leq 200$,当 $n-m$ 较小时,利用上方的求值公式 $O(k^2)$ 求第二类斯特林数,再 $O(n^3)$ 求第一类
CF1521D Nastia Plays with a Tree
题意
给定一颗树,每次操作删去任意一条边并加上任意一条边,求多少次操作后会形成一条链,输出次数及任一方案
解
设答案为 $x$
则删去树上的 $x$ 条边并加上新的 $x$ 条边会构成链
把删去与添加分开看,在删去 $x$ 条边后会形成一个 $x+1$ 棵树的森林,若添加 $x$ 条边能合并为链,则森林由 $x+1$ 条链构成
转化为找到最少分割次数使这棵树形成全为链的森林
设当前在处理点 $i$ ,其有 $c_i$ 个儿子,父节点为 $fa_i$
- 若 $c_i\leq 1$ ,不需任何操作
- 若 $1\leq c_i \leq2$ ,断开 $i$ 与 $fa_i$ 的关系
- 若 $c_i >2$ ,不仅断开 $i$ 与 $fa_i$ ,且断开 $i$ 的任意儿子直至 $c_i\leq 2$
实现的时候注意边的存储
CF1523D Love-Hate
题意
有 $n$ 个人,$m$ 种货币,每个人只喜欢其中不超过 $p$ 种货币,求一种选货币的方案,使选的每一种货币都喜欢的人数不小于 $\lceil\frac{n}{2}\rceil$
解
先去除喜欢人数 $<\lceil\frac{n}{2}\rceil$ 的货币,将枚举的货币状态降至 $2^30$,用 $\text{bitset}$ 存喜欢每一种货币的人的状态,暴力搜索并减去不合法的即可
CF1525E Assimilation IV
题意
给定一些城市与点两两之间距离
每回合随机选择一个城市设立纪念碑,辐射范围随回合数增加而增加,即第 $1$ 回合设立的,在第 $2$ 回合可以辐射到与之距离 $\leq 2$ 的所有点
求所有城市设立纪念碑后所有被辐射到的点的期望值
解
分开算每个点的期望值
若直接求能辐射到该点的城市则情况不易讨论,考虑求补集
对于每个点,不被辐射到需要满足:对于第 $1$ 回合选择距离在 $n+1$ 以外的点,其余回合同理
那么把城市选择顺序视为一个排列,求出不能到达的方案数,最后 $1-$ 并 $\div n!$ 求期望即可
CF1527E Partition Game
题意
定义连续子序列 $t$ 的代价是
$set$ 表示子序列的元素集合,$last,first$ 表示 $x$ 在子序列中最后/第一次出现的位置
给定长度 $n$ 的序列,分成 $k$ 个连续的子序列,求 $\min cost$
解
显然有 $O(kn^2\log n)$ 的朴素转移:
含义明显
考虑优化 $cost$ 的计算过程
首先,$cost$ 具有决策单调性,即 $cost(i,j)+cost(i+1,j+1) \leq cost(i+1,j)+cost(i,j+1)$
证明不是太会,可以枚举一下最优情况分别位于 $(i,j),(i,j+1),(i+1,j),(i+1,j+1)$ 时,能得出结论:右边的总会优于左边
得到决策单调性后考虑分治,枚举 $dp_{mid}$ 的最优决策点
即用 $\text{solve}(l,r,x,y)$ 计算区间 $[l,r]$ ,最优决策点在 $[x,y]$ 间的所有 $dp_i$
对于 $\text{calc}$ 每次调用的时候左端点单增 $\Rightarrow$ 考虑移动双指针指向队首队尾,每次 $O(1)$ 暴力转移
也可以用deque当懒狗
CF1535E Gold Transfer
十分显然的题
题面中 $It’s \ guaranteed \ that \ p_i \ exists \ and \ c_i>c_{p_i}.$ 表明从越靠近根节点开始买值越小
倍增跳 $anc$ 时检查是否有值即可
CF1539E Game with Cards
题意
两个数 $a,b$ 初始为 $0$ ,进行 $n$ 次操作,每次用 $k$ 去替换 $a,b$ 中任意一个,要求操作后满足 $a_{l,i} \leq a \leq b_{l,i} , a_{r,i} \leq b \leq b_{r,i}$
输出是否可以完成所以操作,若可以,输出任一方案
解
先考虑朴素做法
设 $dp_{L,i,j}=1$ 表示第 $i$ 张牌替换左手,第 $j$ 张是上一张用来替换右手的牌
$dp{R,i,j}=1$表示第 $i$ 张牌替换右手,第 $j$ 张是上一张用来替换左手的牌
由于只判断可行性,所以不需要存下所有的 $dp$ 状态,用 $集合f_0 = \left\langle k[j],j\right\rangle$存下 $dp_{L,i,j}=1$ 的情况,$f_1$ 同理
考虑 $f_0 [i]$ 与 $f_1 [i]$ 的计算 $\Rightarrow$ 先考虑 $f_0 [i+1]$ , $f_1 [i+1]$ 同理
先假设第 $i+1$ 张卡可以给左手(确保 $f_0 [i+1]$ 不空) ,且第 $i+1$ 回合右手可以替换为任意卡(稍后再处理)
若 $f_1 [i]$ 不空,可以将 $\langle k[i],i\rangle$ 添加到 $f_0 [i+1]$ 中,即左手拿第 $i+1$ 张使状态 $(j(上一次改变的),i) \Rightarrow (i+1,i)$
同时 $f_0 [i+1]$ 会继承 $f_0 [i]$ 的状态,即 $(i,j) \Rightarrow (i+1,j)$
转移后处理那些无法被成功转移的,由于 $set$ 结构,分别从 $\min$ 和 $\max$ 来 $erase$ 那些 $\leq l$ 或 $\geq r$ 的 $pair$
CF1540B Tree Array
题意简述
一颗树,开始时从中等概率选择一点,随后每次等概率选择一点不与选择过的点重复且与任一选择的点相连。
点编号按选择的先后顺序排序,求期望逆序对数
解
考虑开始时随机选点,显然可以枚举每一点作为根,求出期望值后 $\div n$ 得到
求每个序列中的期望逆序对数,并不需要知道每个序列,即考虑每一对逆序对
设逆序点对为 $(x,y)$ ,其中 $y>x$,当沿树向下进行时,直到 $x,y$ 的 $lca$ 之前概率相等,所以只需要考虑从 $lca$ 到 $x,y$ 两点的概率,即从 $lca$ 先到 $x$ 的概率
参照官方题解,转化成以下模型
存在两个栈,每次有 $p$ 概率弹出 $栈1$ 中的一个,$p$ 的概率弹出 $栈2$ 中的一个,还有 $1-2*p$ 的概率不做任何操作
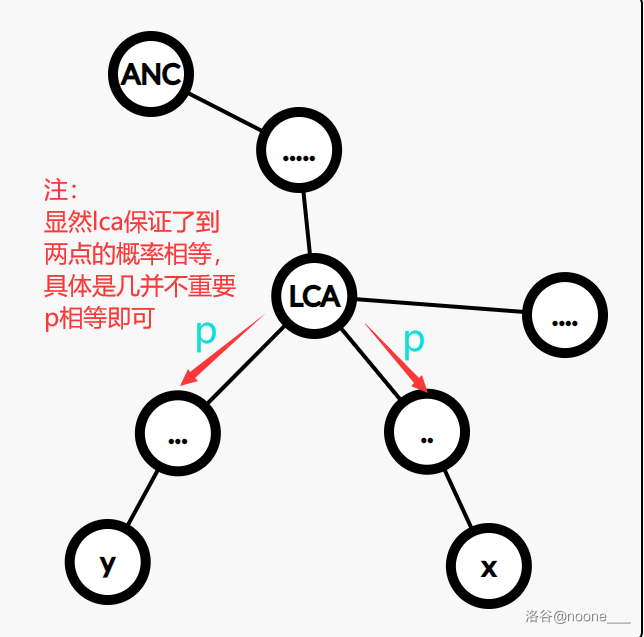
既然满足到 $x,y$ 的概率相等,则可以由上方的值 $\div 2$ 推出
所以可以写出式子
其中 $i,j$ 表示逆序点对与 $lca$ 的距离
$dp_{0,j}=1$ ,即 $i$ 位置代表的点先被到达时会形成逆序点对
至此,流程为:预处理 $dp_{i,j}$ $\Rightarrow$ 枚举根 $\Rightarrow$ 枚举逆序点对并统计 $dp$ 值 $\Rightarrow$ 总值 $\div n$ 得到概率(期望,这里说不清了)
CF1510D Digits
题意
给定 $n$ 个数,求能使其中一些数使其乘积最大且最后一位以 $d$ 结尾. 输出具体方案
解
一个显然的想法是令 $d_{i,j}$ 表示前 $i$ 个数,末位为 $j$ 的最大乘积, $dp$ 转移的时候记录路径即可,可惜会爆 $ll$
一个在模拟赛里见过的 $trick$ 是使用对数
如果 $a>b$ , 那么 $\log(a)>\log(b)$ ,且 $\log(a\times b)=\log(a)+\log(b)$ ,转换成了加法
$\therefore$ 只需记录最大的和
令 $d_{i,j}$ 表示前 $i$ 个数,末位为 $j$ 的最大乘积的 $\log$ 值, $dp$ 转移的时候记录路径即可.
CF372C Watching Fireworks is Fun
题意
$n$ 个区域,编号为 $1\sim n$ ,有 $m$ 个烟花,给定地点 $a_i$ ,时间 $t_i$ ,参数 $b_i$ ,在 $x$ 时能获得 $b_i-|a_i-x|$ 的值
单位时间内能移动 $\leq d$ 个单位长,初始在 $1$ ,求获得的最大值
首先显然有转移:
复杂度 $O(mn^2)$
首先有滚动数组优化降低空间
对于枚举的 $b_i-|a_i-x|$ ,套路的转化为求 $\max\{-|a_i-x|\}$ ,即, $\min\{|a_i-x|\}$
考虑到 $i,j$ 的枚举无法被省略,那么就要考虑维护当前 $k$ 能得到的最小值
那么用单调队列,从左右分别求依次 $f_{i,j}$ 即可