P6962 [NEERC2017]Knapsack Cryptosystem
依据数据范围分成两部分
折半算法 $O(2^{\frac{n}{2}})$
将 $n$ 个数分为 $\left\lfloor \frac{n}{2} \right\rfloor$ 和 $\left\lceil \frac{n}{2} \right\rceil$ 两组,对每组中的每个子集计算和
再枚举其中一组,判断另一组
$O(2^{64-n} \cdot n)$
发现$b_i$ 与 $a_i$ 对应,枚举 $a_1$ 取值并以此解出 $r$ , 再解出 $a_2’,a_3’ \cdots a_n’$
从大到小贪心枚举,判断 $a’$ 是否满足条件
注:
求解 $r$ 时,根据 $a_1\cdot r\equiv b_1\pmod{2^{64}} \quad \text{式1}$
设 $k=\text{__builtin_ctz}(b_1)$ (即,$b_1$ 二进制下末尾 $0$ 的个数)
$\displaystyle{\because r 是奇数 \qquad \text{注:r,q 互质}}$
$\therefore \text{__builtin_ctz}(a_1)=k$
式 $1$ 两边同除以 $2^k$ 得: $a_1 \cdot r \cdot 2^{-k} = b_1 \cdot 2^{-k} \pmod{2^{64}-k}$
$\therefore 得到的 r 只能保证前 64-k 位正确$
$\therefore 再继续枚举后 k 位$
注意到 $a_1$ 末尾恰好有 $k$ 个 $0$,所以枚举的时候每次加上 $2^{k+1}即可$
P6938 [ICPC2017 WF]Son of Pipe Stream
先忽略 $v$ , 因为当 $v\not ={1}$ 时,将 $v=1$ 的答案 $\cdot v^{-\alpha}$ 即可
证:
$\because v\cdot f_i+w_i \leq c_i,\\ \therefore把 v 看成 1 相当于 f_i少算了 \frac{1}{v}$
$\because F^{\alpha}\\ \therefore \cdot v^{-\alpha}$
易知若流 $(F,W)$ 合法,当且仅当 $F\leq F_{max},W\leq W_{max},F+W\leq S$
有解 $(F_{max},S-F_{max})$ 和 $(S-W_{max},W_{max})$
看成增广时优先增广其中一边
设函数 $V(F)=F^{\alpha} \cdot (S-W)^{\alpha}$ , V的最大值就是所求答案
当 $F=\alpha S$ 时 $V$ 有最大值
证明 (%%%@神仙ljr
对 $V$ 求导
当 $V(F)^{\prime}=0$ 时,V有 $\max$
$\therefore F=0 或 F=\alpha C$
所以构造出流 $(F_0,S-F_0)$ ,其中 $F_0$ 是与 $\alpha \cdot S$ 最接近的
实现
分别以 $1,2$ 为源跑一次最大流,得 $Flubber$ 和 $Water$ 的最大流量 $F_{max},W_{max}$
再新建源连向 $1,2$ ,跑一次 $Flubber+Water$ 的最大混合流量 $S$ ,最优的 $F$ 就是在 $[S−W_{max},F_{max}]$ 里最贴近 $\alpha \cdot S$ 的值,于是得到新的 $F^{\prime}$ ,然后 $W^{\prime}=S−F^{\prime}$ ,可以证明这两个流量是一定可以得到且一定是最优的
然后考虑构造解,新建源连向 $1,2$ 容量分别为 $F^{\prime},W^{\prime}$ ,跑一次最大流,然后根据这次结果新建图,新图中每条边的方向就是这次流的方向,容量就是这次的流量
超级源点只连 $1$ 容量 $F^{\prime}$ 跑一次得到每条边 $Flubber$ 的流量,只连 $2$ 容量 $W^{\prime}$ 跑一次得到每条边 $Water$ 的流量
P6944 [ICPC2018 WF]Gem Island
最终状态出现次数相等,均为 $d!$ 次
不同操作方案有 $n\cdot (n+1)\cdot \cdots (n+1-1)=\frac{(n+d-1)!}{(n-1)!}$
先求出不同的最终状态,再进行处理
$\therefore$ 转化为求和为 $n+d$ 的 $n$ 个数,且满足每个数 $\geq$ $1$ 的所有方案的前 $r$ 个数的和
起初每个人都为 $1$ 个,和为 $n$
选 $s_1$ 个人变成 $2$ 个,和为 $n+s_1$,方案数 $\ast$= $\dbinom{n}{s_1}$
在 $s_1$ 个人中选 $s_2$ 个,和为 $n+s_1+s_2$ ,方案数 $\ast$= $\dbinom{s_1}{s_2}$
$\cdots$
每一次对前 $r$ 大的贡献为 $\min(r,s_x)$ ,其中 $s_x$ 为当前加入的个数
P6922 [ICPC2016 WF]Longest Rivers
对于叶子节点 $i$ ,一定有从其到根的一条路径,距离为 $d_i$
要满足剖分 $D$ 中叶子节点 $j$ 所在链长 $l_{D,j} > d_i$ 的链 $l$ 的数量最小
对于每个节点 $i$ ,如果存在一条河流比 $d_i$ 长,那么让它延伸会使答案最小,否则要选择一条最短的河流来进行延伸。
设 $f_i$ 表示每个节点往外延伸的河流的长度的最小值,通过树形DP求。
将 $d$ 升序,临界点自下向上收束,对每个 $d_i$ ,所有超过了上一个 $d$ 的限制,但是满足当前的 $d$ 限制的临界点,这些点将不再是临界点。
若一个点所有的儿子都不是临界点,则它变为临界点。
用堆按 $f$ 从小到大维护临界点,答案就是临界点个数+1,也就是堆中元素个数+1。
P4348 [CERC2015]Cow Confinement
扫描线 显然
考虑从右往左扫,维护 $f_y$:
当 $y+1$ 处是栅栏,$(x,y)$ 处的答案就是 $f_y$
若不是,$f_y$ 是 $(x,y)$ 比 $(x,y+1)$ 多出来的值
看成差分
向下累加 $y$ 直到栅栏
牛 $\Rightarrow$ 查询
花 $\Rightarrow$ $+1$
栅栏 $(x_l,y_l,x_r,y_r)$
在 $x_r$ 处清空 $[y_l,y_r]$ , $y_l-1$ 处加上 $y_l$ 的值,记录 $y_r+1$ 的值
在 $x_l-1$ 处清空 $[y_l,y_r]$ , $y_l-1$ 减去在 $x_r$ 处记录的 $y_r+1$ 的值,防止没有栅栏阻挡而重复计算
P7024 [NWRRC2017]Fygon 2.0
神仙图论题
考虑语句for i in range(a,b):
它创建了变量 $i,a,b$ 并给出它们的大小关系 $a\leq i \ , \ i\leq b$
对于条件 $x\leq y$ ,由 $x$ 向 $y$ 连出有向边
在整张图上,若出现强连通分量就必须满足其中的每个点取值相同(即 $a\leq b\leq c \cdots \leq a$) $\Rightarrow$ 考虑缩点
缩点后得到一个DAG,考虑到有向无环且每个点的值都可以在 $1\to n$ 中取,那么DAG的顶点数即为 $k$
而DAG的一个拓扑序 (即DAG上点的一种大小关系) 对应一个合法的 $k$ 元组
设拓扑序有 $N$,则 $f(n)\geq N \cdot \dbinom{n}{k}$
$\displaystyle{\because \lim_{n \to \infty}\frac{f(n)}{C \cdot n^k}=1 \And \lim_{n \to \infin} \frac{n^{\underline{k}}}{n^k}=1}$
那么 $C=\frac{N}{k!}$
最后用状压求拓扑序个数
注: 输入: I
输出: I
输入: I qwq
输出: I
即,当 cin>>string 时,会因为 [space] 而停止,但不会因为最前面的 space 停止
P7016 [CERC2013]Captain Obvious and the Rabbit-Man
这是人做的?
GG
$f_2,f_3,\cdots ,f_{k+1}$ 互不相同,$\therefore \{a_n\}_{n\geq 1}$ 是一个 $n$ 阶的常系数线性齐次递推数列
特征多项式为 $\displaystyle{P(x)=(x-f_2)\cdot(x-f_3)\cdots(x-f_{k+1})}$
设 $\displaystyle{P(x)=x^k-b_1x^{k-1}-b_2x^{k-2}-\cdots -b_{k-1}x-b_k}$
则 $a_{k+1}=b^1a_k+b_2a_{k-1}+\cdots +b^ka_1$
所以计算出 $P(x)$ 系数再带入即可
P4354 [CERC2015]Ice Igloos
对每个圆,与之相交的直线只会在其周围的4个方格中出现
那么对每个线段,枚举其经过的方格,查看在当前单元格中出现的圆是否与该直线相交
垃圾暴力复杂度 $\Theta(m\ast 4\ast 1000)$ 但够过了
实现好烦
P7054 [NWRRC2015]Graph
神仙图论题
贪心,从开头到末尾依次贪心,让第一个位置的字典序最大,再让第二个最大
对某个拓扑层来说,需要对该点中最小节点加边
用一个最大堆存暂时无法连边的节点,之后无法拓扑时从中取出顶,将拓扑序的结尾点连向该顶
P4351 [CERC2015]Frightful Formula
题意
求 $f_{n,n}$
取模 $1e6+3$
解
先考虑 $c=0$
该情况是典型的格路计数
从 $(1,1)$ 到 $(n,m)$ 的路径数为 $\displaystyle{C_{n+m-2}^{n-1}}$
证:
一条 $(1,1)$ 到 $(n,m)$ 的自由路可以唯一对应到一个含有 $n-1$ 个右步 $L$ 和 $m-1$ 个下步 $U$ 的序列
每个这种序列也可唯一对应一条自由路
$\therefore$ $(n,m)$ 自由路的条数等于从 $n+m-2$ 个位置中选出 $n-1$ 个 $L$ 的方案数
考虑右步贡献 $\ast a$ , 下步贡献 $\ast b$
$\therefore$ 总贡献是 $C_{n+m-2}^{n-1}\cdot a^{n-1}\cdot b^{m-1}$
由于第一行/列初始贡献不同,所以对每个起点都要计算
考虑 $c\not ={0}$
考虑消掉常数 $c$
找到 $x$ 满足 $x=ax+bx+c$ , 则设 $g_{i,j}=f_{i,j}-x=a\cdot (f_{i,j-1}-x)+b\cdot (f_{i-1,j}-x)$
将 $g_{n,n}$ 用上面的方法求出再加上 $x=\frac{c}{1-a-b}$ 即可
观察 $x$ 的值,仅当 $a+b \not\equiv 1\pmod {10^6+3}$
式子转化为 $f_{i,j}=a\cdot f_{i,j-1}+(1-a)f_{i-1,j}+c$
此时两项系数和相等,下标和相等,所以考虑一个与 $i+j$ 有关的函数 $h_{i,j}$
易得 $h_{i,j}=k\cdot (i+j)=k\cdot (i+j-1)+c$ , $\therefore k=c$
$\therefore (f_{i,j}-h_{i,j})=a\cdot(f_{i,j-1}-h_{i,j-1})+(1-a)\cdot(f_{i-1,j}-h_{i-1,j})$
令 $g_{i,j}=f_{i,j}-h_{i,j}$ ,用最上面的方法求 $g_{n,n}$ ,最后加上 $2n\cdot c$
P6943 [ICPC2018 WF]Conquer The World
具体思想可参考 $\text{WC}2019$ 论文
把需要军队的地方称为老鼠,军队为洞,转化为使所有老鼠进洞的总代价最小
为每一个老鼠设一个额外代价 $-\infty$ ,其中 $-\infty$ 是一个足够小的数,表示该老鼠和某个洞匹配后的代价。
因为会最小化总代价,可以保证所有老鼠进洞
只需要最后把答案加上 $-\infty \cdot M$ 即可,其中 $M$ 是老鼠个数
记节点 $i$ 到根的距离为 $depth_i$ ,树上 $Lca$ 为 $z$ 的点 $x,y$ 之间的路径长度为 $depth_x+depth_y-2\times depth_z$
考虑在 $z$ 子树中的所有老鼠和洞,仅需要数值,而不关心具体位置
上述额外代价 $-\infty$ 可与 $depth_x$ 或 $depth_y$ 累加,看做固有属性,记为 $value_x,value_y$
每当我们找到可以使当前总代价减小的匹配,即 $value_x+value_y-2\times depth_z<0$ 的匹配,选取,答案将会变优
但这样找到的匹配可能不是最终答案 $\Rightarrow$ 需要一个反悔
考虑撤销本次匹配的代价,我们可以重新计算得到新的 $value’_x=2\times depth_z-value’_y,value’_y=2\times depth_z-value_x$
所以解法:即从叶子结点出发,向上进行贪心
用两个小根堆来维护子树内 $value_x,value_y$ 的集合,在合并两棵子树的同时合并它们对应的堆。当堆顶元素满足 $value_x+value_y-2\times depth_z<0$ 时更新答案,并删除堆顶元素,加入 $value’_x,value’_y$
可以发现,若一对已经在 $z$ 处匹配的老鼠和洞同时反悔,那么 $z$ 的父边将会被老鼠正反经过两次,因此不反悔是更优的,从而不可能出现同时反悔的情况
P6899 [ICPC2014 WF]Pachinko
模型是网格图的随机游走
考虑高斯消元,有 $w\cdot h$ 个未知数,对网格 $(i,j)$ 可以设值为 $X_{i\ast w+j}$
则有公式 $X_{i\ast w+j}=u\cdot X_{w\ast (i-1)+j} + l\cdot X_{w\ast i+(j-1)} + r\cdot X_{w\ast i-(j+1)} + d\cdot X_{w\ast (i+1)+j} + P_{直接选到该格子}$
其中
考虑高斯消元
每个方程只有 $5$ 个未知数,则有值的位置形成了一个带状矩阵
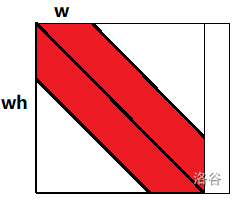
偷一张卢神的图
$\therefore$ 一个未知数只有上 $w$ 行与下 $w$ 行之间的系数不为 $0$
P7011 [CERC2013]Escape
神仙题
先考虑最简单的链情况
$blood$ 的变化为 $w_1,w_1+w_2,w_1+w_2+w_3+\cdots ,w_1+w_2+\cdots+w_n$,只有当所有数均 $\geq 0$ 时游戏胜利
做一条折线图反映血量变化
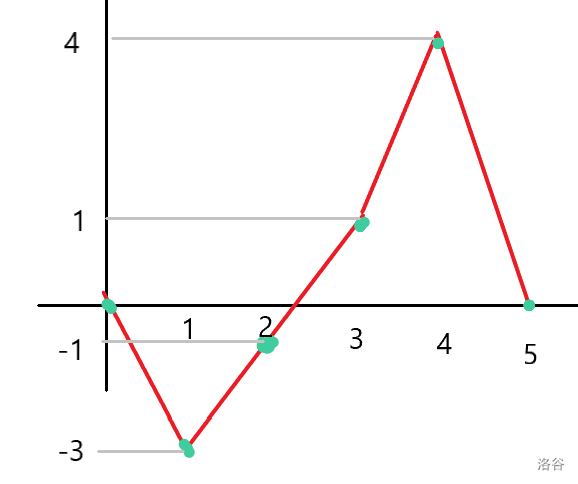
可以发现中间的部分对我们没有用,有用的是最低值(决定了是否可行),以及最终能得到的最高值(中间的加减可忽略掉)
所以可以处理得到
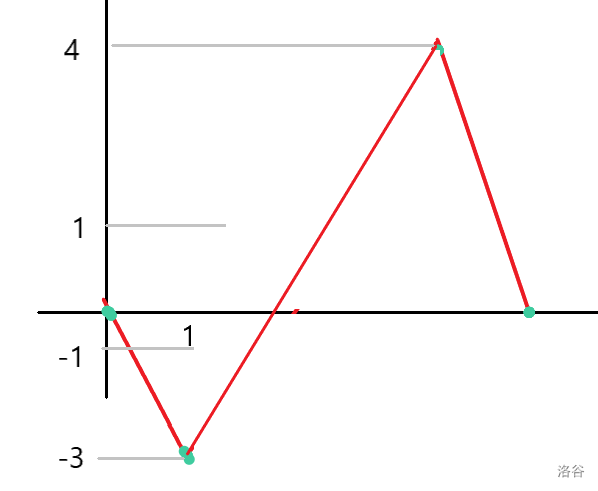
所以维护这个链上所能得到的最大前缀和以及最小前缀和即可
所以可以把一条链简化成一个 $pair$ 数组 $[(a_1,b_1),(a_2,b_2),\cdots]$
注意:这里 $a_1,b_1$ 等都是正数
表示折线方向为 $-a_1+b_1-a_2+b_2\cdots$ ,为统一,规定 $a_1$ 一定向下
再考虑树上
每棵树总可分成多条链来考虑,只考虑两条链即可
设两条链分别为 $[(a_1,b_1),(a_2,b_2),\cdots]$ 和 $[(c_1,d_1),(c_2,d_2),\cdots]$ ,
显然第一步走 $\min(a_1,c_1)$ 是一个不劣的选择考虑向 $[(a_1,b_1),(a_2,b_2),\cdots]$ 中插入一个 $pair (x,y)$
应该放到最后一个满足 $a_i < x$ 的位置的后面,原因是靠前会影响前缀最小值,使无法继续向下走;靠后则不能充分利用走该处所带来的 $-x+y$ 的优势
具体实现
- 使最终能到 $t$ 点,则设 $t$ 点权值 $\text{INF}$
- 显然 $t$ 的子树不需要考虑
- 选用了 $\text{map}$ 存放 $\text{pair}$ ,即 $mp[a_i]=b_i$
P6970 [NEERC2016]Game on Graph
概括题意:
设 $v_A$ 表示在节点 $v$ 且 $A$ 先手,$v_B$ 同理
用 $\N+(v)$ 表示 $v$ 通过一条边可到达的所有点集合
定义 $\N+(v_A)$ 中的点表示下一轮轮到 $B$
先考虑无限循环
对点 $v_A$ 来说,无限循环需要满足 $\exist v_B\in \N+(v_A)$ 使 $v_B$ 无限进行
对点 $v_B$ 来说,需要满足 $\N+(v_B) \not =\empty \And\And \forall v_A\in \N+(v_B)$ 都有 $v_A$ 满足无限循环
出度为 $0$ 的点可以在刚开始时分出胜负,那么不断迭代即可
考虑胜负
将所有无限进行的状态从图中删去,得到新图,若一个点存在先负的后继状态,则它一定是先胜;若一个点的所有后继状态都是先胜 (含没有后继状态),则它是先负。
如果遇到圈则一定为 $A$ 赢
P6932 [ICPC2017 WF]Money for Nothing
题意
这道题有个很妙的题意转化
即给定 $m$ 个 $A$ 点的坐标(表示生产商), $n$ 个 $B$ 点的坐标(消费商),求一个边与坐标轴平行的矩形,其以 $A$ 类点为右上角, $B$ 类点为左下角,且其面积最大
先考虑显然的单调性
对 $A$ 来说,若存在 $\{x_1,y_1\} , \{x_2,y_2\}$ 满足 $x_2\geq x_1 , y_2\geq y_1$,则只保留 $\{x_2,y_2\}$, $B$ 同理
只维护 $A$ 的左上单调集和 $B$ 的右下单调集
设 $A$ 点 $(x_A,y_A)$,$B$ 点 $(x_B,y_B)$,其形成的矩形面积
易得若有一个 $A$ 点与所有 $B$ 点围成的矩形都为 $-\infty$ 则根据单调性,其余点也只能围成 $-\infty$ 的矩形,故此时答案为 $0$
考虑决策单调性
设 $(x_B,y_B)$ 是与 $A$ 类点 $(x_A,y_A)$ 配对的矩阵面积最大的 $B$ 类点,则对于
有
所以可以考虑整体二分